2015-2016学年甘肃省天水市秦安二中高三上学期期末数学试卷（理科）

试卷更新日期：2016-11-14 类型：期末考试

进入出卷网下载

一、选择题

1. 设U=R，已知集合A={x|x＞1}，B={x|x＞a}，且（∁_UA）∪B=R，则a的范围是（　　）

A、（﹣∞，1） B、（1，+∞） C、（﹣∞，1] D、[1，+∞）

查看试题解析
2. 已知O、A、B、C为同一平面内的四个点，若2 $\vec{A C}$ + $\vec{C B}$ = $\vec{0}$ ，则向量 $\vec{O C}$ 等于（）

A、 $\frac{2}{3} \vec{O A}$ ﹣ $\frac{1}{3}$ $\vec{O B}$ B、﹣ $\frac{1}{3}$ $\vec{O A}$ + $\frac{2}{3}$ $\vec{O B}$ C、2 $\vec{O A}$ ﹣ $\vec{O B}$ D、﹣ $\vec{O A}$ ﹣2 $\vec{O B}$

查看试题解析
3. 已知a，b是实数，则“ ${(\frac{1}{3})}^{a} < {(\frac{1}{3})}^{b}$ ”是“log₃a＞log₃b”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 若命题“∃x₀∈R，使得x₀²+mx₀+2m﹣3＜0”为假命题，则实数m的取值范围是（）

A、[2，6] B、[﹣6，﹣2] C、（2，6） D、（﹣6，﹣2）

查看试题解析
5. 若sin（ $\frac{π}{6}$ ﹣α）= $\frac{1}{3}$ ，则2cos²（ $\frac{π}{6}$ + $\frac{α}{2}$ ）﹣1=（）

A、 $\frac{1}{3}$ B、- $\frac{1}{3}$ C、 $\frac{7}{9}$ D、- $\frac{7}{9}$

查看试题解析
6. 如图所示的程序框图的功能是（）

A、求数列{ $\frac{1}{n}$ }的前10项的和 B、求数列{ $\frac{1}{n}$ }的前11项的和 C、求数列{ $\frac{1}{2 n}$ }的前10项的和 D、求数列{ $\frac{1}{2 n}$ }的前11项的和

查看试题解析
7. 下列函数：①y=xsinx，②y=xcosx，③y=x|cosx|，④y=x2^x的图象（部分）如图（但顺序被打乱）：则从左到右的各图象依次对应的函数序号是（）

A、①④②③ B、①④③② C、④①②③ D、③④②①

查看试题解析
8. 设抛物线C：y²=2px（p＞0）的焦点为F，点M在C上，|MF|=5，若以MF为直径的圆过点（0，2），则C的方程为（　　）

A、y²=4x或y²=8x B、y²=2x或y²=8x C、y²=4x或y²=16x D、y²=2x或y²=16x

查看试题解析
9. 变量x、y满足条件 ${\begin{matrix} x - y + 1 \leq 0 \\ y \leq 1 \\ x > - 1 \end{matrix}$ ，则（x﹣2）²+y²的最小值为（）

A、 $\frac{3 \sqrt{2}}{2}$ B、 $\sqrt{5}$ C、 $\frac{9}{2}$ D、5

查看试题解析
10. 已知非零向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} | = \frac{2 \sqrt{3}}{3} | \vec{a} |$ ，则 $\vec{a} + \vec{b}$ 与 $\vec{a} - \vec{b}$ 的夹角为（）

A、 $\frac{5 π}{6}$ B、 $\frac{π}{6}$ C、 $\frac{2 π}{3}$ D、 $\frac{π}{3}$

查看试题解析
11. 设双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1的两条渐近线与直线x= $\frac{a^{2}}{c}$ 分别交于A，B两点，F为该双曲线的右焦点．若60°＜∠AFB＜90°，则该双曲线的离心率的取值范围是（）

A、（1， $\sqrt{2}$ ） B、（ $\sqrt{2}$ ，2） C、（1，2） D、（ $\sqrt{2}$ ，+∞）

查看试题解析
12. 设函数f（x）=e^x（x³﹣3x+3）﹣ae^x﹣x（x≥﹣2），若不等式f（x）≤0有解，则实数α的最小值为（）

A、 $\frac{2}{e} - 1$ B、2﹣ $\frac{2}{e}$ C、1﹣ $\frac{1}{e}$ D、1+2e²

查看试题解析

二、填空题

13. $\int_{0}^{2}$ （2﹣|1﹣x|）dx= ．

查看试题解析
14. 函数f（x）=2sin（ωx+φ）（ω＞0，﹣ $\frac{π}{2}$ ＜φ＜ $\frac{π}{2}$ ）的部分图象如图所示，则函数f（x）解析式

查看试题解析
15. 已知函数f（x）=lnx﹣ $\frac{m}{x}$ （m∈R）在区间[1，e]取得最小值4，则m= ．

查看试题解析
16. 已知抛物线y²=4x的准线与双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）交于A、B两点，点F为抛物线的焦点，若△FAB为直角三角形，则双曲线离心率的取值范围是．

查看试题解析

三、解答题

17. 已知正项等比数列{a_n}满足a₁ ， 2a₂ ， a₃+6成等差数列，且a₄²=9a₁a₅ ，

(1)、求数列{a_n}的通项公式；

(2)、设b_n=（ $\log_{\sqrt{3}}$ a_n+1）•a_n ，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 某校在2 015年11月份的高三期中考试后，随机地抽取了50名学生的数学成绩并进行了分析，结果这50名同学的成绩全部介于80分到140分之间．现将结果按如下方式分为6组，第一组[80，90），第二组[90，100），…第六组[130，140]，得到如图所示的频率分布直方图．

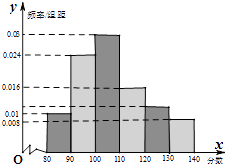(1)、试估计该校数学的平均成绩（同一组中的数据用该区间的中点值作代表）；

(2)、这50名学生中成绩在120分以上的同学中任意抽取3人，该3人在130分（含130分）以上的人数记为X，求X的分布列和期望．

查看试题解析
19. 如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且 $∠ B C D = ∠ B C E = \frac{π}{2}$ ，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2

(1)、证明：AG∥平面BDE；

(2)、求平面BDE和平面BAG所成锐二面角的余弦值．

查看试题解析
20. 椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0），作直线l交椭圆于P，Q两点，M为线段PQ的中点，O为坐标原点，设直线l的斜率为k₁ ，直线OM的斜率为k₂ ， k₁k₂=﹣ $\frac{2}{3}$ ．

(1)、求椭圆C的离心率；

(2)、设直线l与x轴交于点D（﹣ $\sqrt{3}$ ，0），且满足 $\vec{D P}$ =2 $\vec{Q D}$ ，当△OPQ的面积最大时，求椭圆C的方程．

查看试题解析
21. 已知f（x）=xlnx﹣ax，g（x）=﹣x²﹣2．

(1)、对一切x∈（0，+∞），f（x）≥g（x）恒成立，求实数a的取值范围；

(2)、当a=﹣1时，求函数f（x）在区间[m，m+3]（m＞0）上的最值；

(3)、证明：对一切x∈（0，+∞），都有 $\ln x + 1 ＞ \frac{1}{e^{x + 1}} - \frac{2}{e^{2} x}$ 成立．

查看试题解析
22.
如图，在△ABC中，DC⊥AB于D，BE⊥AC于E，BE交DC于点F，若BF=FC=3，DF=FE=2．

(1)、求证：AD•AB=AE•AC；

(2)、求线段BC的长度．

查看试题解析
23. 在极坐标系中，曲线C的方程为 $ρ^{2} = \frac{3}{1 + 2 \cos^{2} θ}$ ，点 $R (2 \sqrt{2} ， \frac{π}{4})$ ，以极点为原点，极轴为x轴的正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位．

(1)、求曲线C的直角坐标方程及点R的直角坐标；

(2)、设P为曲线C上一动点，以PR为对角线的矩形PQRS的一边垂直于极轴，求矩形PQRS周长的最小值及此时点P的直角坐标．

查看试题解析
24. 设不等式﹣2＜|x﹣1|﹣|x+2|＜0的解集为M，a、b∈M，

(1)、证明：| $\frac{1}{3}$ a+ $\frac{1}{6}$ b|＜ $\frac{1}{4}$ ；

(2)、比较|1﹣4ab|与2|a﹣b|的大小，并说明理由．

查看试题解析