难点九立体几何中的折叠问题、最值问题和探索性问题

试卷更新日期：2018-03-02 类型：二轮复习

进入出卷网下载

一、单选题

1.
如图，在等腰梯形ABCD中，AB=2DC=2，∠DAB=60°，E为AB的中点，将△ADE与△BEC分别沿ED、EC向上折起，使A、B重合于点P，则P﹣DCE三棱锥的外接球的体积为（　　）

A、 $\frac{4 \sqrt{3} π}{27}$ B、 $\frac{\sqrt{6} π}{2}$ C、 $\frac{\sqrt{6} π}{8}$ D、 $\frac{\sqrt{6} π}{24}$

查看试题解析
2. 将边长为 $\sqrt{2}$ 的正方形 $A B C D$ 沿对角线 $A C$ 折成一个直二面角 $B - A C - D$ .则四面体 $A B C D$ 的内切球的半径为（）

A、1 B、 $2 \sqrt{2} - \sqrt{3}$ C、 $\sqrt{2} - 1$ D、 $2 - \sqrt{3}$

查看试题解析
3. 如图，在三棱锥A﹣BCD中，已知三角形ABC和三角形DBC所在平面互相垂直，AB=BD，∠CBA=∠CBD= $\frac{2 π}{3}$ ，则直线AD与平面BCD所成角的大小是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{π}{2}$

查看试题解析
4. 已知三棱柱的各侧面均垂直于底面，底面为正三角形，且侧棱长与底面边长之比为2：1，顶点都在一个球面上，若该球的表面积为 $\frac{16}{3}$ π，则此三棱柱的侧面积为（　　）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、8 D、6

查看试题解析
5. 在棱长为6的正方体ABCD﹣A₁B₁C₁D₁中，M是BC的中点，点P是面DCC₁D₁内的动点，且满足∠APD=∠MPC，则三棱锥P﹣BCD的体积最大值是（）

A、36 B、12 $\sqrt{3}$ C、24 D、18 $\sqrt{3}$

查看试题解析
6. 已知边长为 $2 \sqrt{3}$ 的菱形ABCD中，∠A=60°，现沿对角线BD折起，使得二面角A﹣BD﹣C为120°，此时点A，B，C，D在同一个球面上，则该球的表面积为（）

A、20π B、24π C、28π D、32π

查看试题解析
7.
如图，在棱长为1的正方体ABCD﹣A₁B₁C₁D₁中，点E，F分别是棱BC，CC₁的中点，P是侧面BCC₁B₁内一点，若A₁P∥平面AEF，则线段A₁P长度的取值范围是（　　）

A、[1， $\frac{\sqrt{5}}{2}$ ] B、[ $\frac{3 \sqrt{2}}{4}$ ， $\frac{\sqrt{5}}{2}$ ] C、[ $\frac{\sqrt{5}}{2}$ ， $\sqrt{2}$ ] D、[ $\sqrt{2}$ ， $\sqrt{3}$ ]

查看试题解析
8. 如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A'DE是△ADE绕DE旋转过程中的一个图形，则下列命题中正确的是（）
①FA'⊥DE；
②BC∥平面A'DE；
③三棱锥A'﹣FED的体积有最大值．

A、① B、①② C、①②③ D、②③

查看试题解析
9. 一个三棱锥的三视图如图所示，则该三棱锥的四个面的面积中最大的是（）

A、 $\sqrt{14}$ B、 $\sqrt{5}$ C、4 D、3

查看试题解析
10. 将一张边长为12cm的正方形纸片按如图（1）所示阴影部分裁去四个全等的等腰三角形，将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型，如图（2）所示放置．如果正四棱锥的主视图是等边三角形，如图（3）所示，则正四棱锥的体积是（）

A、 $\frac{32}{3} \sqrt{6}$ cm³ B、 $\frac{64}{3} \sqrt{6}$ cm³ C、 $\frac{32}{3} \sqrt{2}$ cm³ D、 $\frac{64}{3} \sqrt{2}$ cm³

查看试题解析
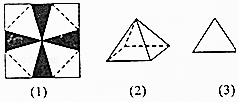11. 如图，已知三棱锥P﹣ABC的底面是等腰直角三角形，且∠ACB= $\frac{π}{2}$ ，侧面PAB⊥底面ABC，AB=PA=PB=2．则这个三棱锥的三视图中标注的尺寸x，y，z分别是（）

A、 $\sqrt{3}$ ，1， $\sqrt{2}$ B、 $\sqrt{3}$ ，1，1 C、2，1， $\sqrt{2}$ D、2，1，1

查看试题解析
12.
如图，二面角的棱上有C、D两点，线段AC、BD分别在这个二面角的两个半平面内，且都垂直于CD ，已知AC=2，BD=3， AB=6，CD= $\sqrt{17}$ ，则这个二面角的大小为( )

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{5 π}{6}$ D、 $\frac{2 π}{3}$

查看试题解析

二、填空题

13.
在三棱锥P﹣ABC中，AB⊥BC，AB=6， $B C = 2 \sqrt{3}$ ，O为AC的中点，过C作BO的垂线，交BO、AB分别于R、D．若∠DPR=∠CPR，则三棱锥P﹣ABC体积的最大值为．

查看试题解析
14. 在正四棱锥V﹣ABCD内有一半球，其底面与正四棱锥的底面重合，且与正四棱锥的四个侧面相切，若半球的半径为2，则当正四棱锥的体积最小时，其高等于．

查看试题解析
15. 已知边长为2 $\sqrt{3}$ 的菱形ABCD中，∠BAD=60°，沿对角边BD折成二面角A﹣BD﹣C为120°的四面体ABCD，则四面体的外接球的表面积为．

查看试题解析
16. 某几何体的一条棱长为3，在该几何体的正视图中，这条棱的投影是长为2的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为．

查看试题解析

三、解答题

17.
如图1，在边长为 $2 \sqrt{3}$ 的正方形ABCD中，E、O分别为 AD、BC的中点，沿 EO将矩形ABOE折起使得∠BOC=120°，如图2所示，点G 在BC上，BG=2GC，M、N分别为AB、EG中点．

（Ⅰ）求证：MN∥平面OBC；
（Ⅱ）求二面角 G﹣ME﹣B的余弦值．

查看试题解析
18. 在如图所示的几何体中，四边形ABCD为正方形，四边形ABEF为直角梯形，且AF∥BE，AB⊥BE，平面ABCD∩平面ABEF=AB，AB=BE=2AF=2．
（Ⅰ）求证：AC∥平面DEF；
（Ⅱ）若二面角D﹣AB﹣E为直二面角，
（ i）求直线AC与平面CDE所成角的大小；
（ ii）棱DE上是否存在点P，使得BP⊥平面DEF？若存在，求出 $\frac{D P}{D E}$ 的值；若不存在，请说明理由．

查看试题解析

四、综合题

19. 在正三角形ABC中，E、F、P分别是﹣AB、AC、BC边上的点，满足AE：EB=CF：FA=CP：PB=1：2（如图1）．将△AEF沿EF折起到△A₁EF的位置，使二面角A₁﹣EF﹣B成直二面角，连结A₁B、A₁P（如图2）．

(1)、求证：A₁E⊥平面BEP；

(2)、求二面角B一A₁P一F的余弦值的大小．

查看试题解析
20. 如图，在等腰梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD， $C F = \sqrt{2}$ ．

(1)、求证：BC⊥平面ACFE；

(2)、点M在线段EF上运动，设平面MAB与平面FCB二面角的平面角为θ（θ≤90°），试求cosθ的取值范围．

查看试题解析

难点九 立体几何中的折叠问题、最值问题和探索性问题

一、单选题

二、填空题

三、解答题

四、综合题

难点九立体几何中的折叠问题、最值问题和探索性问题