难点七 新背景下的概率、统计问题,及统计案例(理)
试卷更新日期:2018-03-02 类型:二轮复习
一、单选题
-
1. 甲、乙、丙三名同学6次数学测试成绩及班级平均分(单位:分)如表:
第一次
第二次
第三次
第四次
第五次
第六次
甲
95
87
92
93
87
94
乙
88
80
85
78
86
72
丙
69
63
71
71
74
74
全班
88
82
81
80
75
77
下列说法错误的是( )
A、甲同学的数学学习成绩高于班级平均水平,且较稳定 B、乙同学的数学成绩平均值是81.5 C、丙同学的数学学习成绩低于班级平均水平 D、在6次测验中,每一次成绩都是甲第一、乙第二、丙第三2. 旅游公司为3个旅游团提供4条旅游线路,每个旅游团只能任选其中一条,则不同的选择方法有( )种.A、24 B、48 C、64 D、813. 已知函数f(x)=sinx+ cosx,当x∈[0,π]时,f(x)≥1的概率为( )A、 B、 C、 D、4. 某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则m+n的值是( )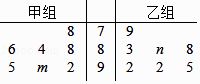 A、10 B、11 C、12 D、135. 某年级有1000名学生,随机编号为0001,0002,…,1000,现用系统抽样方法,从中抽出200人,若0122号被抽到了,则下列编号也被抽到的是( )A、0116 B、0927 C、0834 D、07266. 在区间[﹣2,4]上随机地抽取一个实数x,若x满足x2≤m的概率为 , 则实数m的值为( )A、2 B、3 C、4 D、97. 欧阳修在《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见卖油翁的技艺之高超,若铜钱直径2百米,中间有边长为1百米的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( )A、 B、 C、 D、8. 已知函数g(x)=2cos2x,若在区间[0,π]上随机取一个数x,则事件“g(x)≥ ”发生的概率为( )A、 B、 C、 D、9. 袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取1个球,记下颜色后放回.若连续取三次,用X表示取出红球的个数,则E(X)+D(X)=( )A、2 B、 C、 D、10. 将二项式(x+ )6展开式中各项重新排列,则其中无理项互不相邻的概率是( )A、 B、 C、 D、11. 已知函数f(x)= x3﹣(a﹣1)x2+b2x,其中a∈{1,2,3,4},b∈{1,2,3},则函数f(x)在R上是增函数的概率为( )A、 B、 C、 D、12. 一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
A、10 B、11 C、12 D、135. 某年级有1000名学生,随机编号为0001,0002,…,1000,现用系统抽样方法,从中抽出200人,若0122号被抽到了,则下列编号也被抽到的是( )A、0116 B、0927 C、0834 D、07266. 在区间[﹣2,4]上随机地抽取一个实数x,若x满足x2≤m的概率为 , 则实数m的值为( )A、2 B、3 C、4 D、97. 欧阳修在《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见卖油翁的技艺之高超,若铜钱直径2百米,中间有边长为1百米的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( )A、 B、 C、 D、8. 已知函数g(x)=2cos2x,若在区间[0,π]上随机取一个数x,则事件“g(x)≥ ”发生的概率为( )A、 B、 C、 D、9. 袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取1个球,记下颜色后放回.若连续取三次,用X表示取出红球的个数,则E(X)+D(X)=( )A、2 B、 C、 D、10. 将二项式(x+ )6展开式中各项重新排列,则其中无理项互不相邻的概率是( )A、 B、 C、 D、11. 已知函数f(x)= x3﹣(a﹣1)x2+b2x,其中a∈{1,2,3,4},b∈{1,2,3},则函数f(x)在R上是增函数的概率为( )A、 B、 C、 D、12. 一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )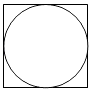 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 在[﹣4,3]上随机取一个数m,能使函数 在R上有零点的概率为 .14. 设a,b为(0,1)上的两个随机数,则满足a﹣2b≤0的概率为
.
15. 设不等式组所表示的区域为M,函数y=sinx,x∈[0,π]的图象与x轴所围成的区域为N,向M内随机投一个点,则该点落在N内的概率为16. 某校举行元旦汇演,七位评委为某班的小品打出的分数如茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差是 .
三、解答题
-
17. 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200.220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.
(Ⅰ)求直方图中x的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
 18. 为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
18. 为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图所示茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.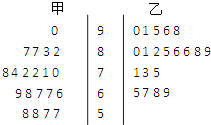 (1)、现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;(2)、学校规定:成绩不低于75分的为优秀.请填写下面的2×2表,并判断有多大把握认为“成绩优秀与教学方式有关”.
(1)、现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;(2)、学校规定:成绩不低于75分的为优秀.请填写下面的2×2表,并判断有多大把握认为“成绩优秀与教学方式有关”.甲班
乙班
合计
优秀
不优秀
合计
下面临界值表仅供参考:
P(x2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.79
10.828
(参考公式:x2= )
19. 襄阳农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数,得到如下数据:日期
12月1日
12月2日
12月3日
12月4日
12月5日
温差x(℃)
10
11
13
12
8
发芽数y(颗)
23
26
32
26
16
襄阳农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)、求选取的2组数据恰好是不相邻的2天数据的概率;(2)、若选取的是12月1日与12月5日这两组数据,情根据12月2日至12月4日的数据,求y关于x的线性回归方程 = x+ ;(3)、若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?注: = = , = ﹣ • .
20. 为响应国家“精准扶贫,产业扶贫”的战略,进一步优化能源消费结构,某市决定在一地处山区的A县推进光伏发电项目.在该县山区居民中随机抽取50户,统计其年用电量得到以下统计表.以样本的频率作为概率.用电量(度)
(0,200]
(200,400]
(400,600]
(600,800]
(800,1000]
户数
5
15
10
15
5
(I)在该县山区居民中随机抽取10户,记其中年用电量不超过600度的户数为X,求X的数学期望;
(II)已知该县某山区自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度进行收购.经测算以每千瓦装机容量年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接收益多少元?