难点三与三角变换、平面向量、函数等综合的三角形问题

试卷更新日期：2018-03-01 类型：二轮复习

进入出卷网下载

一、单选题

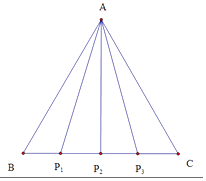
1. 在△ABC中，∠ABC=120°，BA=2，BC=3，D，E是线段AC的三等分点，则 $\vec{B D}$ • $\vec{B E}$ 的值为（）

A、 $\frac{65}{9}$ B、 $\frac{11}{9}$ C、 $\frac{41}{9}$ D、﹣ $\frac{13}{9}$

查看试题解析
2. O为△ABC内一点，且2 $\vec{O A} + \vec{O B} + \vec{O C} = \vec{0}$ ， $\vec{A D}$ =t $\vec{A C}$ ，若B，O，D三点共线，则t的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 在△ABC中，PQ分别是AB，BC的三等分点，且AP= $\frac{1}{3}$ AB，BQ= $\frac{1}{3}$ BC，若 $\vec{A B}$ = $\vec{a}$ ， $\vec{A C}$ = $\vec{b}$ ，则 $\vec{P Q}$ =（　　）

A、 $\frac{1}{3}$ $\vec{a}$ + $\frac{1}{3}$ $\vec{b}$ B、- $\frac{1}{3}$ $\vec{a}$ + $\frac{1}{3}$ $\vec{b}$ C、 $\frac{1}{3}$ $\vec{a}$ - $\frac{1}{3}$ $\vec{b}$ D、- $\frac{1}{3}$ $\vec{a}$ - $\frac{1}{3}$ $\vec{b}$

查看试题解析
4. 在直角△ABC中，∠BCA=90°，CA=CB=1，P为AB边上的点且 $\vec{A P}$ =λ $\vec{A B}$ ，若 $\vec{C P}$ • $\vec{A B}$ ≥ $\vec{P A}$ • $\vec{P B}$ ，则λ的取值范围是（）

A、[ $\frac{1}{2}$ ，1] B、[ $\frac{2 - \sqrt{2}}{2}$ ，1] C、[ $\frac{1}{2}$ ， $\frac{1 + \sqrt{2}}{2}$ ] D、[ $\frac{1 - \sqrt{2}}{2}$ ， $\frac{1 + \sqrt{2}}{2}$ ]

查看试题解析
5. 如图，在等腰直角△ABO中，设 $\vec{O A}$ = $\vec{a}$ ， $\vec{O B}$ = $\vec{b}$ ，| $\vec{O A}$ |=| $\vec{O B}$ |=1，C为AB上靠近A点的三等分点，过C作AB的垂线l，设P为垂线上任一点， $\vec{O P}$ = $\vec{p}$ ，则 $\vec{p}$ •（ $\vec{b}$ ﹣ $\vec{a}$ ）=（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、﹣ $\frac{3}{2}$ D、 $\frac{3}{2}$

查看试题解析
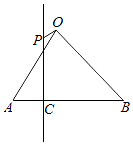6. 已知△ABC的外接圆半径为1，圆心为O，且3 $\vec{O A} + 4 \vec{O B} + 5 \vec{O C} = \vec{0}$ ，则△ABC的面积为（）

A、 $\frac{8}{5}$ B、 $\frac{7}{5}$ C、 $\frac{6}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 若集合中三个元素为边可构成一个三角形，则该三角形一定不可能是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
8. △ABC中，角A，B，C所对的边分别为a，b，c，若c＜bcosA，则△ABC为（）

A、钝角三角形 B、直角三角形 C、锐角三角形 D、不确定

查看试题解析
9. 已知△ABC中，D为边BC上靠近B点的三等分点，连接AD，E为线段AD的中点，若 $\vec{C E} = m \vec{A B} + n \vec{A C}$ ，则m+n=（）

A、 $- \frac{1}{3}$ B、 $- \frac{1}{2}$ C、 $- \frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
10. 已知P为△ABC内一点，且满足 $\vec{P A} + 2 \vec{P B} + \vec{P C} = \vec{0}$ ，记△ABP，△BCP，△ACP的面积依次为S₁ ， S₂ ， S₃ ，则S₁：S₂：S₃等于（）

A、1：2：3 B、1：4：9 C、2：3：1 D、3：1：2

查看试题解析
11. △DEF的外接圆的圆心为O，半径R=4，如果 $\vec{O D} + \vec{D E} + \vec{D F} = 0$ ，且 $| \vec{O D} | = | \vec{D F} |$ ，则向量 $\vec{E F}$ 在 $\vec{F D}$ 方向上的投影为（）

A、6 B、﹣6 C、 $2 \sqrt{3}$ D、- $2 \sqrt{3}$

查看试题解析
12. 已知点O为△ABC内一点，∠AOB=120°，OA=1，OB=2，过O作OD垂直AB于点D，点E为线段OD的中点，则 $\vec{O E}$ • $\vec{E A}$ 的值为（）

A、 $\frac{5}{14}$ B、 $\frac{2}{7}$ C、 $\frac{3}{14}$ D、 $\frac{3}{28}$

查看试题解析

二、填空题

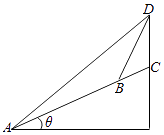
13. 已知O是△ABC外接圆的圆心，已知△ABC外接圆半径为2，若 $4 \vec{O A} + 5 \vec{O B} + 6 \vec{O C} = \vec{0}$ ，则边长AB= ．

查看试题解析
14. 如图所示，在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD，为了测量该山坡相对于水平地面的坡角θ，在山坡的A处测得∠DAC=15°，沿山坡前进50m到达B处，又测得∠DBC=45°，根据以上数据可得cosθ= ．

查看试题解析
15. 某中学举行升旗仪式，在坡度为15°的看台E点和看台的坡脚A点，分别测得旗杆顶部的仰角分别为30°和60°，量的看台坡脚A点到E点在水平线上的射影B点的距离为10cm，则旗杆的高CD的长是 m．

查看试题解析
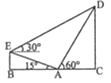16. 在△ABC中，内角A，B，C的对边分别为a，b，c，且a＞b，a＞c．△ABC的外接圆半径为1， $a = \sqrt{3}$ ，若边BC上一点D满足BD=2DC，且∠BAD=90°，则△ABC的面积为．

查看试题解析

三、综合题

17. 如图所示，已知点G是△ABO的重心．

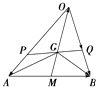(1)、求 $\vec{G A}$ + $\vec{G B}$ + $\vec{G O}$ ；

(2)、若PQ过△ABO的重心G，且 $\vec{O A}$ = $\vec{a}$ ， $\vec{O B}$ = $\vec{b}$ ， $\vec{O P}$ =m $\vec{a}$ ， $\vec{O Q}$ =n $\vec{b}$ ，求证： $\frac{1}{m}$ + $\frac{1}{n}$ =3．

查看试题解析
18. △ABC的三个内角A，B，C的对边分别a，b，c，已知 $\vec{m} = (\frac{cosB}{b} + \frac{cosC}{c} ， \sin A)$ ， $\vec{n} = (\frac{1}{a} ， 1)$ ，且 $\vec{π}$ ∥ $\vec{n}$

(1)、证明sinBsinC=sinA；

(2)、若a²+c²﹣b²= $\frac{10}{13}$ ac，求tanC．

查看试题解析
19. 设△ABC是边长为4的正三角形，点P₁ ， P₂ ， P₃ ，四等分线段BC（如图所示）

(1)、P为边BC上一动点，求 $\vec{P A}$ • $\vec{P C}$ 的取值范围？

(2)、Q为线段AP₁上一点，若 $\vec{A Q}$ =m $\vec{A B}$ + $\frac{1}{12}$ $\vec{A C}$ ，求实数m的值．

查看试题解析
20. 已知向量 $\vec{m} = (\sqrt{2} c o s \frac{x}{4} ， 2 c o s \frac{x}{4})$ ， $\vec{n} = (\sqrt{2} c o s \frac{x}{4} ， \sqrt{3} s i n \frac{x}{4})$ ，设 $f (x) = \vec{m} \cdot \vec{n}$ ．
（Ⅰ）若f（α）=2，求 $c o s (α + \frac{π}{3})$ 的值；
（Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a﹣b）cosC=ccosB，求f（A）的取值范围．

查看试题解析

难点三 与三角变换、平面向量、函数等综合的三角形问题

一、单选题

二、填空题

三、综合题

难点三与三角变换、平面向量、函数等综合的三角形问题