高中数学人教新课标A版必修2 第二章点、直线、平面之间的位置关系 2.3.3直线与平面垂直的性质

试卷更新日期：2018-02-27 类型：同步测试

进入出卷网下载

1. 正方体 $A B C D - A^{'} B^{'} C^{'} D^{'}$ 中，E为A′C′的中点，则直线CE垂直于（）

A、A′C′ B、BD C、A′D′ D、AA′

查看试题解析
2. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，直线 $l$ （与直线BB₁不重合）⊥平面A₁C₁,则有（）

A、B₁B⊥l B、B₁B∥l C、B₁B与l异面 D、B₁B与l相交

查看试题解析
3. 已知l⊥平面α，直线m⊂平面β.有下面四个命题：
①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β；④l⊥m⇒α∥β.
其中正确的命题是（）

A、①② B、③④ C、②④ D、①③

查看试题解析
4. 如图，平行四边形ABCD中，AB⊥BD.沿BD将△ABD折起，使面ABD⊥面BCD，连接AC，则在四面体ABCD的四个面所在平面中，互相垂直的平面的对数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 在空间四边形ABCD中，平面ABD⊥平面BCD，且DA⊥平面ABC，则△ABC是（）

A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

查看试题解析

6. 如图，在斜三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，∠BAC=90°，BC₁⊥AC，则点C₁在平面ABC上的射影H必在（）

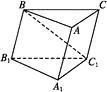A、直线AB上 B、直线BC上 C、直线AC上 D、△ABC的内部

查看试题解析
7. 如图所示，已知六棱锥 $P - A B C D E F$ 的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论正确的是（）

A、PB⊥AD B、平面PAB⊥平面PBC C、直线BC∥平面PAE D、直线PD与平面ABC所成的角为45°

查看试题解析
8. 在棱长都相等的四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，则下面四个结论中不成立的是（）

A、BC∥平面PDF B、DF⊥平面PAE C、平面PDF⊥平面ABC D、平面PAE⊥平面ABC

查看试题解析

9. 如图所示，沿直角三角形ABC的中位线DE将平面ADE折起，使得平面ADE⊥平面BCDE，得到四棱锥 $A - B C D E$ ，则平面ABC与平面ACD的关系是.

查看试题解析
10. 如图，已知平面α∩平面β=l，EA⊥α，垂足为A，EB⊥β，垂足为B，直线a⊂β，a⊥AB，则直线a与直线l的位置关系是.

查看试题解析
11. 如图所示，平面ABC⊥平面ABD，∠ACB=90°，CA=CB，△ABD是正三角形，则二面角 $C - B D - A$ 的平面角的正切值为.

查看试题解析

12. 如图，四棱柱ABCD－A₁B₁C₁D₁的底面ABCD是正方形，O为底面中心，A₁O⊥平面ABCD，AB＝AA₁＝ $\sqrt{2}$ .证明：A₁C⊥平面BB₁D₁D.

查看试题解析
13. 如图，在四棱锥 $P - A B C D$ 中，平面PAD⊥ABCD，AB=AD，∠BAD=60°，E，F分别是AP，AD的中点.
求证：

(1)、直线EF∥平面PCD；

(2)、平面BEF⊥平面PAD.

查看试题解析
14. 如图所示，在平行四边形ABCD中，已知AD＝2AB＝2a，BD＝ $\sqrt{3} a$ ，AC∩BD＝E，将其沿对角线BD折成直二面角．
求证：

(1)、AB⊥平面BCD；

(2)、平面ACD⊥平面ABD.

查看试题解析

高中数学人教新课标A版必修2 第二章 点、直线、平面之间的位置关系 2.3.3直线与平面垂直的性质