辽宁省鞍山市2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2018-02-26 类型：期末考试

进入出卷网下载

一、单选题

1. 在函数 $y = {(x + 1)}^{2} + 3$ 中， $y$ 随 $x$ 增大而减小，则 $x$ 的取值范围为（）

A、 $x$ ＞－1 B、 $x$ ＞3 C、 $x$ ＜－1 D、 $x$ ＜3

查看试题解析
2. 如图，点A是反比例函数图象的一点，自点A向 $y$ 轴作垂线，垂足为T，已知 $S_{Δ A O T} = 4$ ，则此函数的表达式为（）

A、 $y = - \frac{4}{x}$ B、 $y = \frac{8}{x}$ C、 $y = - \frac{16}{x}$ D、 $y = - \frac{8}{x}$

查看试题解析
3. 已知：如图，四边形ABCD是⊙O的内接正方形，点P是CD弧上不同于点C的任意一点，则∠BPC的度数是（）

A、45° B、60° C、75° D、90°

查看试题解析
4. 将点P（－2，3）向右平移3个单位得到点P₁ ，点P₂与点P₁关于原点对称，则P₂的坐标是（）

A、（－5，－3） B、（1，－3） C、（－1，－3） D、（5，－3）

查看试题解析
5. 关于 $x$ 的一元二次方程 $x^{2} + 2 (m - 1) x + m^{2} = 0$ 的两个实数根分别为 $x_{1}$ ， $x_{2}$ ，且 $x_{1} + x_{2} > 0 ， x_{1} \cdot x_{2} > 0$ ，则 $m$ 的取值范围是（）

A、 $m \leq \frac{1}{2}$ B、 $m \leq \frac{1}{2}$ 且 $m \neq 0$ C、 $m < 1$ D、 $m < 1$ 且 $m \neq 0$

查看试题解析
6. 如图，边长为2的正三角形ABO的边OB在x轴上，将△ABO绕原点O逆时针旋转30°得到正三角形OA₁B₁ ，则点A₁的坐标为（）

A、 $(\sqrt{3} ， 1)$ B、 $(\sqrt{3} ， - 1)$ C、 $(1 ， - \sqrt{3})$ D、 $(2 ， - 1)$

查看试题解析
7.
如图，已知△ABC，P为AB上一点，连接CP，以下条件中不能判定△ACP∽△ABC的是（　　）

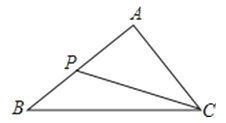A、∠ACP=∠B B、∠APC=∠ACB C、 $\frac{A C}{A P} = \frac{A B}{A C}$ D、 $\frac{A C}{A B} = \frac{C P}{B C}$

查看试题解析
8. 如图，正方形ABCD中，AB＝8 $c m$ ，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以 $1 \frac{c m}{s}$ 的速度沿BC，CD运动，到点C，D时停止运动．设运动时间为 $t (s)$ ，△OEF的面积为S( $c m^{2}$ )，则S( $c m^{2}$ )与 $t (s)$ 的函数关系可用图象表示为（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 将抛物线 $y = x^{2}$ 图象向右平移2个单位再向下平移3个单位，所得图象的解析式为．

查看试题解析
10. 已知2是关于 $x$ 的一元二次方程 $x^{2} + 4 x - p = 0$ 的一个根，则该方程的另一个根是．

查看试题解析
11. 如图所示，△ABC中，DE∥BC，AE∶EB＝2∶3，若△AED的面积是4 $m^{2}$ ，则四边形DEBC的面积为．

查看试题解析
12. 一个边长为4 $c m$ 的等边三角形ABC与⊙O等高，如图放置，⊙O与BC相切于点C，⊙O与AC相交于点E，则CE的长为cm

查看试题解析
13. 反比例函数的图象经过点P（－1，3），则此反比例函数的解析式为．

查看试题解析
14. 如图，正方形ABCD的边长为3，点E是DC边上一点，DE=1，将线段AE绕点A旋转，使点E落在直线BC上，落点记为F，则FC的长为．

查看试题解析
15. 如图，在平面直角坐标系 $x o y$ 中，⊙P与 $y$ 轴相切于点C，⊙P的半径是4，直线 $y = x$ 被⊙P截得的弦AB的长为 $4 \sqrt{3}$ ，则点P的坐标为．

查看试题解析
16. 如图，点 $P_{1} (x_{1} ， y_{1})$ ，点 $P_{2} (x_{2} ， y_{2})$ ， $P_{3} (x_{3} ， y_{3})$ 都在函数 $y = \frac{k}{x} (x > 0)$ 的图象上，△P₁OA₁ ， △P₂A₁A₂ ， △P₃A₂A₃都是等腰直角三角形，斜边OA₁ ， A₁A₂ ， A₂A₃都在 $x$ 轴上，已知点P₁的坐标为（1，1），则点P₃的坐标为．

查看试题解析

三、解答题

17. 解方程： $2 x^{2} + 3 x - 5 = 0$ ．

查看试题解析
18. 已知△ABC在平面直角坐标系中的位置如图所示．

(1)、分别写出图中点A和点C的坐标；

(2)、画出△ABC绕点C按顺时针方向旋转90°后的△ $A^{'} B^{'} C$ ；

(3)、求点A旋转到点 $A^{'}$ 所经过的路线长（结果保留π）．

查看试题解析
19. 如图，在平行四边形ABCD中，对角线AC、BD交于点O．M为AD中点，连接CM交BD于点N，且ON=1．

(1)、求BD的长；

(2)、若△DCN的面积为2，求四边形ABCM的面积．

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $m x^{2} - (m - 1) x - 1 = 0$ ．

(1)、求证：这个一元二次方程总有两个实数根；

(2)、若 $x_{1}$ ， $x_{2}$ 是关于 $x$ 的一元二次方程 $m x^{2} - (m - 1) x - 1 = 0$ 的两根，且 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} = 2 x_{1} x_{2} + 1$ ，求 $m$ 的值．

查看试题解析
21. 已知：如图．在平面直角坐标系 $x o y$ 中，直线AB分别与 $x$ ， $y$ 轴交于点B、A，与反比例函数的图象分别交于点C、D，CE⊥ $x$ 轴于点E， $\frac{A O}{B O} = \frac{1}{2}$ ，OB=4，OE=2．

(1)、求该反比例函数的解析式；

(2)、求△BOD的面积．

查看试题解析
22. 如图，AB是⊙O的直径，点C在⊙O上，CD与⊙O相切，AD∥BC，连结OD，AC．

(1)、求证：∠B=∠DCA；

(2)、若 $\frac{A C}{B C} = \frac{\sqrt{5}}{2}$ ，OD= $3 \sqrt{6}$ ，求⊙O的半径长．

查看试题解析
23. 某宾馆有客房200间供游客居住，当每间客房的定价为每天180元时，客房恰好全部住满；如果每间客房每天的定价每增加10元，就会减少4间客房出租．设每间客房每天的定价增加x元，宾馆出租的客房为y间．求：

(1)、y关于x的函数关系式；

(2)、如果某天宾馆客房收入38400元，那么这天每间客房的价格是多少元？

查看试题解析
24. 如图，排球运动员站在点O处练习发球，将球从O点正上方2 $m$ 的A处发出，把球看成点，其运行的高度 $y (m)$ 与运行的水平距离 $x (m)$ 满足关系式 $y = a {(x - 6)}^{2} + h$ ．已知球网与O点的水平距离为9 $m$ ，高度为2.43 $m$ ，球场的边界距O点的水平距离为18 $m$ ．

(1)、当 $h$ =2.6时，求 $y$ 与 $x$ 的关系式（不要求写出自变量 $x$ 的取值范围）；

(2)、当 $h$ =2.6时，球能否越过球网？球会不会出界？请说明理由；

(3)、若球一定能越过球网，又不出边界，求二次函数中 $h$ 的取值范围．

查看试题解析
25. 如图，△ABC中，AB=AC，AD∥BC，CD⊥AC，连BD，交AC于E．

(1)、如图1，若∠BAC=60°，求 $\frac{A E}{B C}$ 的值；

(2)、如图2，CF⊥AB于F，交BD于G，求证：CG=FG

查看试题解析
26. 已知：在平面直角坐标系中，抛物线 $y = a x^{2} + x$ 的对称轴为直线 $x = 2$ ，顶点为A．

(1)、求抛物线的表达式及顶点A的坐标；

(2)、点P为抛物线对称轴上一点，联结OA、OP．
①当OA⊥OP时，求OP的长；
②过点P作OP的垂线交对称轴右侧的抛物线于点B，联结OB，当∠OAP=∠OBP时，求点B的坐标．

查看试题解析