河北省廊坊市三河市2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2018-02-26 类型：期末考试

进入出卷网下载

一、单选题

1. 如果分式 $\frac{1}{1 - x}$ 有意义，那么x的取值范围是（）

A、x＞1 B、x＜1 C、x≠1 D、x=1

查看试题解析
2. 在平面直角坐标系中，点P（2，3）关于x轴的对称点坐标为（）

A、（﹣2，3） B、（2，﹣3） C、（3，﹣2） D、（﹣2，﹣3）

查看试题解析
3. 下列计算中，正确的是（）

A、x³÷x=x² B、a⁶÷a²=a³ C、x•x³=x³ D、x³+x³=x⁶

查看试题解析
4. 如图所示，在下列条件中，不能判断△ABD≌△BAC的条件是（）

A、∠D=∠C，∠BAD=∠ABC B、∠BAD=∠ABC，∠ABD=∠BAC C、BD=AC，∠BAD=∠ABC D、AD=BC，BD=AC

查看试题解析
5. 如图，在平面直角坐标系中，点A在第一象限，点P在x轴上，若以P，O，A为顶点的三角形是等腰三角形，则满足条件的点P共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 某工厂计划生产210个零件，由于采用新技术，实际每天生产零件的数量是原计划的1.5倍，因此提前5天完成任务．设原计划每天生产零件x个，依题意列方程为（）

A、 $\frac{210}{x}$ ﹣ $\frac{210}{1.5 x}$ =5 B、 $\frac{210}{x}$ ﹣ $\frac{210}{x - 1.5}$ =5 C、 $\frac{210}{1.5 + x}$ ﹣ $\frac{210}{x}$ =5 D、 $\frac{210}{5} = 1.5 + \frac{210}{x}$

查看试题解析
7. PM2.5是指大气中直径≤0.0000025米的颗粒物，将0.0000025用科学记数法表示为（）.

A、2.5×10^-7 B、2.5×10^-6 C、25×10^-7 D、0.25×10^-5

查看试题解析
8. 如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A等于（）

A、30° B、40° C、45° D、36°

查看试题解析
9. 在各个内角都相等的多边形中，一个外角等于一个内角的 $\frac{1}{2}$ ，则这个多边形的边数是（）

A、5 B、6 C、7 D、8

查看试题解析
10. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（）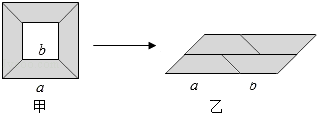

A、a²﹣b²=（a﹣b）² B、（a+b）²=a²+2ab+b² C、（a﹣b）²=a²﹣2ab+b² D、a²﹣b²=（a+b）（a﹣b）

查看试题解析

二、填空题

11. 分解因式：2x²﹣2= ．

查看试题解析
12. 计算：（﹣ $\frac{5}{3}$ ）^﹣2= ．

查看试题解析
13. 化简： $\frac{m - 1}{m}$ ÷ $\frac{m - 1}{m^{2}}$ = ．

查看试题解析
14. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S_△ABC=4cm² ，则S_阴影=cm² ．

查看试题解析
15. 如图，点P为∠AOB内一点，分别作出点P关于OA、OB的对称点P₁、P₂ ，连接P₁P₂交OA于M，交OB于N，若P₁P₂=6，则△PMN的周长为．

查看试题解析
16. 二次三项式x²﹣kx+9是一个完全平方式，则k的值是．

查看试题解析
17. 若m²﹣2m﹣1=0，则代数式2m²﹣4m+3的值为．

查看试题解析
18. 观察下列式子：
3²﹣1²=8=8×1；
5²﹣3²=16=8×2；
7²﹣5²=24=8×3；
9²﹣7²=32=8×4；
用公式将你所发现的规律用含n（n为正整数）的代数式表示出来．

查看试题解析

三、解答题

19. 计算题：分式与分式方程

(1)、计算：x÷（x﹣1）• $\frac{x}{x - 1}$

(2)、解方程： $\frac{2}{x - 1} + \frac{x}{1 - x}$ =1．

查看试题解析
20. 如图，点B、E、C、F在一条直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．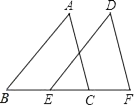

查看试题解析
21. 先化简，再求值： $(1 - \frac{1}{x + 1}) \div \frac{x}{x^{2} - 1}$ ，其中x=﹣ $\frac{3}{2}$ ．

查看试题解析
22. 如图，分别过点C、B作△ABC的BC边上的中线AD及其延长线的垂线，垂足分别为E、F．求证：BF=CE．

查看试题解析
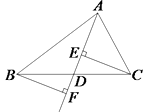23. 如图△ABC是等边三角形，BD是中线，延长BC到E，使CE=CD．求证：DB=DE．

查看试题解析
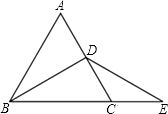24. 一项工程，甲乙两公司合作，12天可以完成，如果甲乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，求甲乙两公司单独完成这项工程，各需多少天？

查看试题解析
25. 如图，小强在河的一边，要测河面的一只船B与对岸码头A的距离，他的做法如下：
①在岸边确定一点C，使C与A，B在同一直线上；
②在AC的垂直方向画线段CD，取其中点O；
③画DF⊥CD使F、O、A在同一直线上；
④在线段DF上找一点E，使E与O、B共线．
他说测出线段EF的长就是船B与码头A的距离．他这样做有道理吗？为什么？

查看试题解析
26. 在数学探究课上，老师出示了这样的探究问题，请你一起来探究：
已知：C是线段AB所在平面内任意一点，分别以AC，BC为边，在AB同侧作等边三角形ACE和BCD，联结AD，BE交于点P．

(1)、如图1，当点C在线段AB上移动时，线段AD与BE的数量关系是：．

(2)、如图2，当点C在直线AB外，且∠ACB＜120°，上面的结论是否还成立？若成立请证明，不成立说明理由．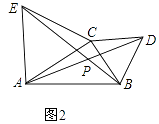

(3)、在（2）的条件下，∠APE的大小是否随着∠ACB的大小的变化而发生变化，若变化，写出变化规律，若不变，请求出∠APE的度数．

查看试题解析