2015-2016学年山东省临沂市郯城县七年级上学期期末数学试卷

试卷更新日期：2016-11-11 类型：期末考试

进入出卷网下载

一、选择题

1. 在数1，0，﹣1，﹣2中，最小的数是（）

A、1 B、0 C、﹣1 D、﹣2

查看试题解析
2. 如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）

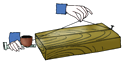A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
3. 把方程 $\frac{1}{2}$ x=1变形为x=2，其依据是（）

A、分数的基本性质 B、等式的性质1 C、等式的性质2 D、解方程中的移项

查看试题解析
4. 下列说法正确的是（）

A、整式就是多项式 B、π是单项式 C、x⁴+2x³是七次二项次 D、 $\frac{3 x - 1}{5}$ 是单项式

查看试题解析
5. 已知a＞b且a+b=0，则（）

A、a＜0 B、b＞0 C、b≤0 D、a＞0

查看试题解析
6. 如果|a|=|b|，那么a，b两个实数一定是（）

A、都等于0 B、一正一负 C、相等 D、相等或互为相反数

查看试题解析
7. 已知关于x的方程2x﹣m﹣5=0的解是x=﹣2，则m的值为（）

A、9 B、﹣9 C、1 D、﹣1

查看试题解析
8. 已知a﹣b=3，c+d=2，则（b+c）﹣（a﹣d）的值是（）

A、﹣1 B、1 C、﹣5 D、15

查看试题解析
9. 解方程1﹣ $\frac{x + 3}{6} = \frac{x}{2}$ ，去分母，得（）

A、1﹣x﹣3=3x B、6﹣x﹣3=3x C、6﹣x+3=3x D、1﹣x+3=3x

查看试题解析
10. 点A、B、C在同一条数轴上，其中点A、B表示的数分别为﹣3、1，若BC=2，则AC等于（　　）

A、3 B、2 C、3或5 D、2或6

查看试题解析
11. 按如图的运算程序，能使输出结果为3的x，y的值是（）

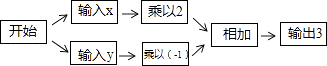A、x=5，y=﹣2 B、x=3，y=﹣3 C、x=﹣4，y=2 D、x=﹣3，y=﹣9

查看试题解析
12. 已知面包店的面包一个15元，小明去此店买面包，结账时店员告诉小明：“如果你再多买一个面包就可以打九折，价钱会比现在便宜45元”，小明说：“我买这些就好了，谢谢．”根据两人的对话，判断结账时小明买了多少个面包？（）

A、38 B、39 C、40 D、41

查看试题解析
13. 如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD=150°，则∠BOC等于（）

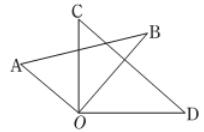A、30° B、45° C、50° D、60°

查看试题解析
14. 甲乙两人各用一张正方形的纸片ABCD折出一个45°的角（如图），两人做法如下：
甲：将纸片沿对角线AC折叠，使B点落在D点上，则∠1=45°；
乙：将纸片沿AM、AN折叠，分别使B、D落在对角线AC上的一点P，则∠MAN=45°．
对于两人的做法，下列判断正确的是（）

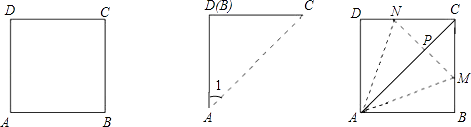A、甲乙都对 B、甲对乙错 C、甲错乙对 D、甲乙都错

查看试题解析

二、填空题

15. 如果一个角的度数为31°42′，那么它的补角的度数为°．

查看试题解析
16. 在检测排球质量过程中，规定超过标准的克数为正数，不足的克数记为负数，根据下表提供的检测结果，你认为质量最接近标准的是号排球．

查看试题解析
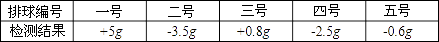17. 在实数范围定义运算“&”：a&b=2a+b，则满足x&（x﹣6）=0的实数x是．

查看试题解析
18. 如果代数式5a+3b的值为﹣4，那么代数式2（a+b）+4（2a+b）的值为．

查看试题解析
19. 小明从家里骑自行车到学校，每小时骑15千米，可早到10分钟；每小时骑12千米，就会迟到5分钟．问他家到学校的路程是多少千米？设他家到学校的路程为x千米，则根据题意列出的方程是．

查看试题解析

三、解答题

20. 计算：

(1)、 $(- \frac{2}{3}) + (- \frac{1}{4}) + (- \frac{3}{4}) + 1 \frac{2}{3}$ ；

(2)、 $- 2^{2} + | - 7 | - 3 - 2 \times (- \frac{1}{2})$ ．

查看试题解析
21. 先化简，再求值：4（x﹣y）﹣2（3x+y）+1，其中 $x = 1 ， y = - \frac{1}{3}$ ．

查看试题解析
22. 解方程：

(1)、10+4（x﹣3）=2x﹣1；

(2)、 $\frac{1}{2} y + 1 = \frac{4 y - 2}{5} - y$ ．

查看试题解析
23. 2012年，某地开始实施农村义务教育学校营养计划﹣﹣“蛋奶工程”．该地农村小学每份营养餐的标准是质量为300克，蛋白质含量为8%，包括一盒牛奶、一包饼干和一个鸡蛋．已知牛奶的蛋白质含量为5%，饼干的蛋白质含量为12.5%，鸡蛋的蛋白质含量为15%，一个鸡蛋的质量为60克．

(1)、一个鸡蛋中含蛋白质的质量为多少克？

(2)、每份营养餐中牛奶和饼干的质量分别为多少克？

查看试题解析
24. 如图，线段AB，C是线段AB上一点，M是AB的中点，N是AC的中点．

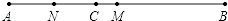(1)、若AB=8cm，AC=3.2cm，求线段MN的长；

(2)、若BC=a，试用含a的式子表示线段MN的长．

查看试题解析
25. 用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）．
A方法：剪6个侧面； B方法：剪4个侧面和5个底面．
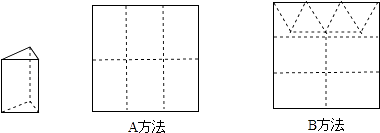
现有19张硬纸板，裁剪时x张用A方法，其余用B方法．

(1)、用x的代数式分别表示裁剪出的侧面和底面的个数；

(2)、若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

查看试题解析
26. 如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=120°．将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．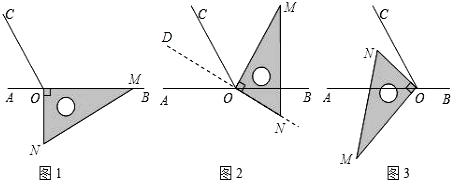

(1)、将图1中的三角板绕点O逆时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC．问：此时直线ON是否平分∠AOC？请说明理由．

(2)、将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，求∠AOM﹣∠NOC的度数．

查看试题解析