2015-2016学年广西南宁市马山县七年级下学期期末数学试卷

试卷更新日期：2016-11-11 类型：期末考试

进入出卷网下载

一、选择题

1. 如图所示是“福娃欢欢”的五幅图案，②，③，④，⑤哪一个图案可以通过平移图案①得到（）

A、② B、③ C、④ D、⑤

查看试题解析
2. 下列调查工作需采用全面调查方式的是（）

A、环保部门对淮河某段水域的水污染情况的调查 B、电视台对正在播出的某电视节目收视率的调查 C、质监部门对各厂家生产的电池使用寿命的调查 D、调查乘坐飞机的旅客是否携带违禁物品

查看试题解析
3. 点P（m+3，m+1）在直角坐标系的x轴上，则P点的坐标为（）

A、（0，﹣2） B、（2，0） C、（0，2） D、（0，﹣4）

查看试题解析
4. 下列式子中，正确的是（）

A、 $\sqrt{- 5}$ =﹣ $\sqrt{5}$ B、 $\sqrt{{(- 3)}^{2}}$ =3 C、 $\sqrt{36}$ =±6 D、± $\sqrt{9}$ =3

查看试题解析
5. 下列说法正确的是（）

A、4的平方根是2 B、 $\sqrt[3]{8}$ 是无理数 C、无限小数都是无理数 D、实数和数轴上的点一一对应

查看试题解析
6. 地理老师介绍到：长江比黄河长836米，黄河长度的6倍比长江长度的5倍多1284千米，小东根据地理教师的介绍，设长江长为x千米，黄河长为y千米，那么下面列出的方程组正确的是（）

A、 ${\begin{matrix} x + y = 836 \\ 5 x - 6 y = 1284 \end{matrix}$ B、 ${\begin{matrix} x - y = 836 \\ 6 x - 5 y = 1284 \end{matrix}$ C、 ${\begin{matrix} x + y = 836 \\ 6 x - 5 y = 1284 \end{matrix}$ D、 ${\begin{matrix} x - y = 836 \\ 6 y - 5 x = 1284 \end{matrix}$

查看试题解析
7. 已知a＜b，则下列不等式中不正确的是（）

A、4a＜4b B、a+4＜b+4 C、﹣4a＜﹣4b D、a﹣4＜b﹣4

查看试题解析
8. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（）

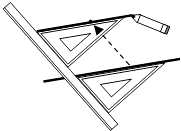A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、两直线平行，同位角相等

查看试题解析
9. 若关于x的一元一次不等式组 ${\begin{matrix} 3 - 2 x > 1 \\ x - a > 0 \end{matrix}$ 恰有3个整数解，那么a的取值范围是（）

A、﹣2＜a＜1 B、﹣3＜a≤﹣2 C、﹣3≤a＜﹣2 D、﹣3＜a＜﹣2

查看试题解析
10. 如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（）

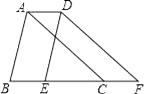A、16cm B、18cm C、20cm D、22cm

查看试题解析

二、填空题

11. 64的立方根为．

查看试题解析
12. 剧院里5排2号可以用（5，2）表示，则（7，4）表示．

查看试题解析
13. 不等式﹣4x≥﹣12的正整数解为．

查看试题解析
14. 如图，把小河里的水引到田地A处就作AB⊥l，垂足为B，沿AB挖水沟，水沟最短．理由是．

查看试题解析
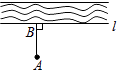15. 由方程3x﹣2y﹣6=0可得到用x表示y的式子是．

查看试题解析
16. 如图，将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上，如果∠1=27°，那么∠2=°．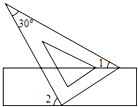

查看试题解析

三、解答题

17. 计算： $\sqrt{{(- 1)}^{2}}$ + $\sqrt[3]{- 27}$ +| $\sqrt{3}$ -2|

查看试题解析
18. 解方程组： ${\begin{matrix} 3 x - y = 7 \\ 5 x + 2 y = 8 \end{matrix}$ ．

查看试题解析
19. 解不等式组： ${\begin{matrix} x - 3 (x - 3) \geq 4 \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ 并把解集在数轴上表示出来．

查看试题解析
20. 如图，已知A（﹣2，2），B（﹣3，﹣2），C（3，﹣2）把△ABC向上平移4个单位长度，再向右平移2个单位得到△A₁B₁C₁ ，解答下列各题：

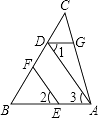
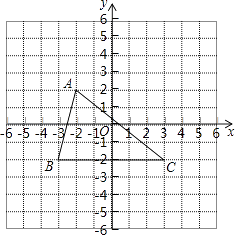(1)、在图上画出△A₁B₁C₁；

(2)、写出点的A₁ ， B₁的坐标；

(3)、求出△A₁B₁C₁的面积．

查看试题解析
21.
如图，EF∥AD，∠1=∠2．说明：∠DGA+∠BAC=180°．请将说明过程填写完成．
解：∵EF∥AD，（已知）
∴∠2= ．（）
又∵∠1=∠2，（）
∴∠1=∠3，（）
∴AB∥ ，（）
∴∠DGA+∠BAC=180°．（）

查看试题解析
22. 如图，AB和CD相交于点O，∠C=∠COA，∠D=∠BOD，判断AC与BD的位置关系，并说明理由．

查看试题解析
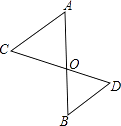23. 我市中小学全面开展“阳光体育”活动，某校在大课间中开设了A：体操，B：跑操，C：舞蹈，D：健美操四项活动，为了解学生最喜欢哪一项活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：

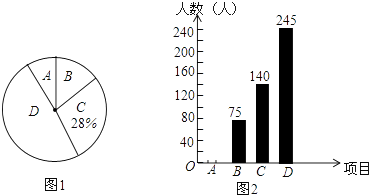(1)、这次被调查的学生共有人．

(2)、请将统计图2补充完整．

(3)、统计图1中B项目对应的扇形的圆心角是度．

(4)、已知该校共有学生3600人，请根据调查结果估计该校喜欢健美操的学生人数．

查看试题解析
24. 为创建“美丽乡村”，某村计划购买甲、乙两种树苗共400棵，对本村道路进行绿化改造，已知甲种树苗每棵200元，乙种树苗每棵300元．

(1)、若购买两种树苗的总金额为90000元，求需购买甲、乙两种树苗各多少棵？

(2)、若购买甲种树苗的金额不少了购买乙种树苗的金额，则至少应购买甲种树苗多少棵？

查看试题解析