2015-2016学年广东省揭阳市普宁市七年级下学期期末数学试卷
试卷更新日期:2016-11-11 类型:期末考试
一、选择题
-
1. 下列各组角中,∠1与∠2是对顶角的为( )A、
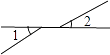 B、
B、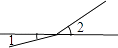 C、
C、 D、
D、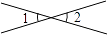 2. 若□×2xy=16x3y2 , 则□内应填的单项式是( )A、4x2y B、8x3y2 C、4x2y2 D、8x2y3. 计算(6×103)•(8×105)的结果是( )A、48×109 B、48×1015 C、4.8×108 D、4.8×1094. 下列计算正确的是( )A、(﹣x3)2=﹣x6 B、(﹣x2)3=﹣x6 C、x6÷x3=x2 D、x3•x4=x125. 下面四个图形中,线段BE是△ABC的高的图是( )A、
2. 若□×2xy=16x3y2 , 则□内应填的单项式是( )A、4x2y B、8x3y2 C、4x2y2 D、8x2y3. 计算(6×103)•(8×105)的结果是( )A、48×109 B、48×1015 C、4.8×108 D、4.8×1094. 下列计算正确的是( )A、(﹣x3)2=﹣x6 B、(﹣x2)3=﹣x6 C、x6÷x3=x2 D、x3•x4=x125. 下面四个图形中,线段BE是△ABC的高的图是( )A、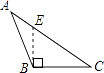 B、
B、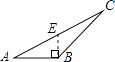 C、
C、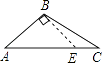 D、
D、 6. 甲和乙一起做游戏,下列游戏规则对双方公平的是( )A、在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋中任意摸出一球,摸到红球甲获胜,摸到白球乙获胜; B、从标有号数1到100的100张卡片中,随意抽取一张,抽到号数为奇数甲获胜,否则乙获胜; C、任意掷一枚质地均匀的骰子,掷出的点数小于4则甲获胜,掷出的点数大于4则乙获胜; D、让小球在如图所示的地板上自由地滚动,并随机地停在某块方块上,若小球停在黑色区域则甲获胜,若停在白色区域则乙获胜
6. 甲和乙一起做游戏,下列游戏规则对双方公平的是( )A、在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋中任意摸出一球,摸到红球甲获胜,摸到白球乙获胜; B、从标有号数1到100的100张卡片中,随意抽取一张,抽到号数为奇数甲获胜,否则乙获胜; C、任意掷一枚质地均匀的骰子,掷出的点数小于4则甲获胜,掷出的点数大于4则乙获胜; D、让小球在如图所示的地板上自由地滚动,并随机地停在某块方块上,若小球停在黑色区域则甲获胜,若停在白色区域则乙获胜 7. 下列各式不能运用平方差公式计算的是( )A、(﹣x﹣y)(﹣x+y) B、(﹣x+y)(x﹣y) C、(x+y)(x﹣y) D、(y+x)(x﹣y)8. 下列各式计算正确的是( )A、(m﹣n)2=m2﹣n2 B、(m+2)2=m2+2m+4 C、( ﹣m)2= ﹣m+m2 D、(﹣m+n)2=m2+2mn+n29. 如图,等腰△ABC中,AB=AC,沿直线MN折叠,使点A与点B重合,折痕MN与AC交于点D,已知∠DBC=15°,则∠A的度数是( )
7. 下列各式不能运用平方差公式计算的是( )A、(﹣x﹣y)(﹣x+y) B、(﹣x+y)(x﹣y) C、(x+y)(x﹣y) D、(y+x)(x﹣y)8. 下列各式计算正确的是( )A、(m﹣n)2=m2﹣n2 B、(m+2)2=m2+2m+4 C、( ﹣m)2= ﹣m+m2 D、(﹣m+n)2=m2+2mn+n29. 如图,等腰△ABC中,AB=AC,沿直线MN折叠,使点A与点B重合,折痕MN与AC交于点D,已知∠DBC=15°,则∠A的度数是( )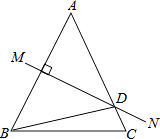 A、50° B、45° C、30° D、15°
A、50° B、45° C、30° D、15°二、填空题
-
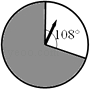
10. 已知等腰三角形的两条边分别是3,6,则第三边的长为 .11. 计算:(﹣18a2b+10b2)÷(﹣2b)= .12. 如图,转动的转盘停止转动后,指针指向黑色区域的概率是 .
 13. 如图,点B在AE上,∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是: . (答案不唯一,写一个即可)
13. 如图,点B在AE上,∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是: . (答案不唯一,写一个即可)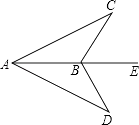 14. 已知圆锥的底面半径是2cm,那么圆锥的体积V(cm3)与高h(cm)的关系式是15. 如图,Rt△ABC中,∠B=90°,CD是∠BCA的平分线,DE⊥AC于E,AC=10,BC=6,则AE= .
14. 已知圆锥的底面半径是2cm,那么圆锥的体积V(cm3)与高h(cm)的关系式是15. 如图,Rt△ABC中,∠B=90°,CD是∠BCA的平分线,DE⊥AC于E,AC=10,BC=6,则AE= .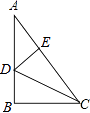
三、解答题(一)
-
16. 计算:[(3a+b)2﹣b2]÷a.17. 化简求值:3x2+(﹣ x+ y2)(2x﹣ y),其中x=﹣ ,y= .18. 已知∠MAN.(1)、用尺规完成下列作图:(保留作图痕迹,不写作法)
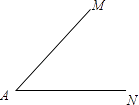
①作∠MAN的平分线AE;
②在AE上任取一点F,作AF的垂直平分线分别与AM、AN交于P、Q;
(2)、在(1)的条件下,线段AP与AQ有什么数量关系,请直接写出结论.四、解答题(二)
-
19. 手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.(1)、判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)、记金额最多、居中、最少的红包分别为A,B,C.①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
20. 把下列的推理过程补充完整,并在括号里填上推理的依据:如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.
试说明:DF∥AB
解:因为BE是∠ABC的角平分线
所以(角平分线的定义)
又因为∠E=∠1(已知)
所以∠E=∠2()
所以()
所以∠A+∠ABC=180°()
又因为∠3+∠ABC=180°(已知)
所以(同角的补角相等)
所以DF∥AB()
 21. 如图,在△ABC中,∠C=90°,点D是AB边上的一点,DE⊥AB于D,交AC于M,且ED=AC,过点E作EF∥BC分别交AB、AC于点F、N.
21. 如图,在△ABC中,∠C=90°,点D是AB边上的一点,DE⊥AB于D,交AC于M,且ED=AC,过点E作EF∥BC分别交AB、AC于点F、N. (1)、试说明:△ABC≌△EFD;(2)、若∠A=25°,求∠EMN的度数.
(1)、试说明:△ABC≌△EFD;(2)、若∠A=25°,求∠EMN的度数.五、解答题(三)
-
22. 陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学离家距离与时间的关系示意图.根据图中提供的信息回答下列问题:
 (1)、陈杰家到学校的距离是米?陈杰在书店停留了分钟?本次上学途中,陈杰一共行驶了米?(2)、在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?(3)、如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?23. 观察下列各式:
(1)、陈杰家到学校的距离是米?陈杰在书店停留了分钟?本次上学途中,陈杰一共行驶了米?(2)、在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?(3)、如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?23. 观察下列各式:(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1;
(x8﹣1)÷(x﹣1)=x7+x6+x5+…+x+1;
(1)、根据上面各式的规律填空:①(x2016﹣1)÷(x﹣1)=
②(xn﹣1)÷(x﹣1)=
(2)、利用②的结论求22016+22015+…+2+1的值;(3)、若1+x+x2+…+x2015=0,求x2016的值.24. 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.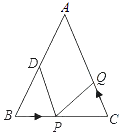 (1)、如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)、如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)、若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?