2015-2016学年北京市东城区七年级上学期期末数学试卷

试卷更新日期：2016-11-11 类型：期末考试

进入出卷网下载

一、选择题

1. ﹣2016的相反数是（）

A、﹣2016 B、2016 C、±2016 D、 $\frac{1}{2016}$

查看试题解析
2. 在3，2，﹣1，﹣4这四个数中，比﹣2小的数是（）

A、﹣4 B、﹣1 C、2 D、3

查看试题解析
3. 近年来，中国高铁发展迅速，高铁技术不断走出国门，成为展示我国实力的新名片．预计到2015年底，中国高速铁路营运里程将达到18000公里．将18000用科学记数法表示应为（）

A、18×10³ B、1.8×10³ C、1.8×10⁴ D、1.8×10⁵

查看试题解析
4. 若∠A=35°16′，则其余角的度数为（）

A、54°44′ B、54°84′ C、55°44′ D、144°44′

查看试题解析
5. 如图，已知OC是∠AOB内部的一条射线，∠AOC=30°，OE是∠COB的平分线．当∠BOE=40°时，∠AOB的度数是（）

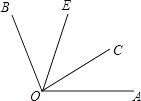A、70° B、80° C、100° D、110°

查看试题解析
6. 与﹣2x²y合并同类项后得到5x²y的是（）

A、﹣3x²y B、3x²y C、7yx² D、7xy²

查看试题解析
7. 某商品的标价为800元，4折销售仍可赚60元，则该商品的进价为（）

A、92元 B、260元 C、320元 D、740元

查看试题解析
8. 已知实数a，b在数轴上的位置如图所示，下列结论错误的是（）

A、|a|＜1＜|b| B、1＜﹣a＜b C、1＜|a|＜b D、﹣b＜a＜﹣1

查看试题解析
9.
如图是正方体的一个平面展开图，如果原正方体上“友”所在的面为前面，则“信”与“国”所在的面分别位于（）

A、上，下 B、右，后 C、左，右 D、左，后

查看试题解析
10. 观察下列关于x的单项式，探究其规律：2x，4x² ， 6x³ ， 8x⁴ ， 10x⁵ ， 12x⁶ ， …，按照上述规律，第2016个单项式是（）

A、2016x²⁰¹⁵ B、2016x²⁰¹⁶ C、4032x²⁰¹⁵ D、4032x²⁰¹⁶

查看试题解析

二、填空题

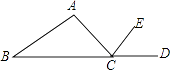
11. 请写出一个只含有x，y两个字母，次数为5，系数是负数的单项式．

查看试题解析
12. 已知关于x的方程3a+x=﹣ $\frac{x}{2}$ ﹣3的解为2，则a的值是．

查看试题解析
13. 在0，﹣3，5， $\frac{1}{3}$ ，π，2.6 $\begin{matrix} \cdot \\ 3 \end{matrix}$ ，1.212 112 111 211 112…六个数中，有理数是．

查看试题解析
14. 若（a+2）²+|b﹣1|=0，则（b+a）²⁰¹⁵= ．

查看试题解析
15. 若数轴上点A表示的数是1，则与点A距离为2的点所表示的数是．

查看试题解析
16. 如图，点D在△ABC边BC的延长线上，CE平分∠ACD，∠A=80°，∠B=40°，则∠ACE的大小是度．

查看试题解析
17. 为庆祝抗日战争胜利70周年，某校初一（1）班举行了主题班会，有20名同学共做了52张纪念卡，其中女生每人做3张，男生每人做2张．问女生和男生各有几人做纪念卡．设女生有x人，男生有y人，根据题意，可列方程组为．

查看试题解析
18. 若一个角的补角比它的余角的2倍多15°，则这个角的度数是．

查看试题解析
19. 定义运算“*”，规定x*y=ax²+by，其中a、b为常数，且1*2=5，2*1=6，则2*3= ．

查看试题解析
20. 已知线段AB=6cm，点C在直线AB上，到点A的距离为3cm，则线段BC的长度为 cm．

查看试题解析

三、解答题

21. 化简：（ $\frac{1}{2}$ a﹣ $\frac{2}{3}$ b）﹣（ $\frac{5}{2}$ a+ $\frac{5}{6}$ b）．

查看试题解析
22. 计算：（2﹣ $\frac{3}{2}$ +| $\frac{1}{3}$ ﹣2|）×（﹣6）．

查看试题解析
23. 计算：（﹣2）³+（﹣3）×[（﹣4）²+2]﹣（﹣3）²÷（﹣2）

查看试题解析
24. 先化简，再求代数式的值：
（xy﹣2xy²）﹣（﹣3x²y²+2xy）﹣（3xy﹣2xy²），其中x= $\frac{2}{3}$ ，y=﹣2．

查看试题解析

四、解答题

25. 解方程：1﹣ $\frac{x - 1}{4}$ = $\frac{2 x + 1}{6}$ ．

查看试题解析
26. 已知线段AB，利用无刻度的直尺和圆规，作线段AC，使点B为线段AC的中点，要求：不写作法，保留作图痕迹．

查看试题解析
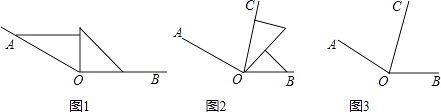
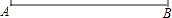27. 数学课上，老师要求同学们用一副三角板画一个钝角，并且画出它的角平分线．小强的作法如下：
①先按照图1的方式摆放一副三角板，画出∠AOB；
②在∠AOB处，再按照图2的方式摆放一副三角板，画出射线OC；
③去掉三角板后得到的图形如图3．
老师说小强的作法完全符合要求．
请你回答：

(1)、小强画的∠AOB的度数是；

(2)、射线OC是∠AOB的平分线的依据是．

查看试题解析
28. 列方程或方程组解应用题：
某小区为改善居住环境，计划在小区内种植甲、乙两种花木共6600棵，若甲种花木的数量是乙种花木数量的2倍少300棵．甲、乙两种花木的数量分别是多少棵？

查看试题解析
29. 将一副三角板按如图方式进行摆放，请判断∠1，∠2是否互补，并说明理由．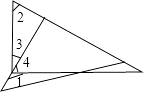

查看试题解析
30. 已知数轴上三点A，O，B表示的数分别为﹣3，0，1，点P为数轴上任意一点，其表示的数为x．

(1)、如果点P到点A，点B的距离相等，那么x=；

(2)、当x=时，点P到点A，点B的距离之和是6；

(3)、若点P到点A，点B的距离之和最小，则x的取值范围是；

(4)、在数轴上，点M，N表示的数分别为x₁ ， x₂ ，我们把x₁ ， x₂之差的绝对值叫做点M，N之间的距离，即MN=|x₁﹣x₂|．若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时，点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动，且三个点同时出发，那么运动秒时，点P到点E，点F的距离相等．

查看试题解析