初二上学期2.4——3.3数学期中复习试卷
试卷更新日期：2016-11-10 类型：期中考试
一、单选题
-
1. 如图，△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC ， 若AD=6，则CD是（ ）
A、1 B、2 C、3 D、42. 如果关于x的不等式（m+1）x＞m+1的解集为x＜1，则m的取值范围是（ ）A、m<0 B、m<-1 C、m>-1 D、m是任意实数.3. 下列说法正确的是( )A、x＝1是不等式－2x＜1的解集 B、x＝-3是不等式－x＜1的解集 C、x＞－2是不等式－2x＜1的解集 D、不等式－x＜1的解集是x＜－14. 已知等腰三角形一腰上的高线等于腰长的一半，那么这个等腰三角形的一个底角等于（ ）A、15°或75° B、15° C、75° D、150°和30°5.一个不等式组的解集在数轴上的表示如下图，则这个不等式组的解集是( )
A、x<3 B、x≥－1 C、－1<x≤3 D、－1≤x<36.如图，在ΔABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M， 交AC于N，若BM+CN=9，则线段MN的长为（ ）
A、6 B、7 C、8 D、97. 用反证法证明命题“一个三角形中至多有一个角是直角”，应先假设这个三角形中（ ）．A、至少有两个角是直角 B、没有直角 C、至少有一个角是直角 D、有一个角是钝角，一个角是直角8.如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（ ）
A、4 B、6 C、8 D、109.如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（ ）
A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC10.如图，正方形网格中的每个小正方形边长都是1．已知A、B是两格点，若△ABC为等腰三角形，且S△ABC=1.5，则满足条件的格点C有（ ）
A、1个 B、2个 C、3个 D、4个11. 数学表达式①﹣5＜7；②3y﹣6＞0；③a=6；④2x﹣3y；⑤a≠2；⑥7y﹣6＞y+2，其中是不等式的有（ ）A、2个 B、3个 C、4个 D、5个12.一个正方形和两个等边三角形的位置如图所示，若∠1=50°，则∠2+∠3=（ ）
A、190° B、130° C、100° D、80°13. 用反证法证明：在一个三角形中，至少有一个内角小于或等于60°，可以假设（ ）A、每个内角都小于60° B、每个内角都大于60° C、至少有一个内角小于或等于60° D、以上答案都不对二、填空题
-
14. 小军的期末总评成绩由平时、期中、期末成绩按权重比1：1：8 组成，现小军平时考试得90分，期中考试得60分，要使他的总评成绩不低于79分，那么小军的期末考试成绩x满足的条件是15.
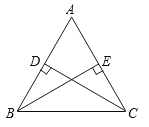
如图，BE，CD是△ABC的高，且BD＝EC，判定△BCD≌△CBE的依据是“”．
16. 下列判断中，正确的序号为 ．①若﹣a＞b＞0，则ab＜0；②若ab＞0，则a＞0，b＞0；③若a＞b，c≠0，则ac＞bc；④若a＞b，c≠0，则ac2＞bc2；⑤若a＞b，c≠0，则﹣a﹣c＜﹣b﹣c．
17.如图所示，∠B=∠D=90°，要证明△ABC与△ADC全等，还需要补充的条件是 ．（填上一个条件即可）
18.如图，MN∥PQ，AB⊥PQ，点A、D、B、C分别在直线MN与PQ上，点E在AB上，AD+BC=7，AD=EB，DE=EC，则AB=
19.如图所示，在△ABC中，∠C=90° ， AD平分∠BAC ， BC=20cm ， DB=17cm ， 则D点到AB的距离是cm．
20. 不等式组 的解集是 ．
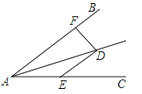
21.如图：∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于 ．
22. 若关于x、y的二元一次方程组的解满足x+y＞1，则k的取值范围是23. 直角三角形中，两直角边长分别为12和5，则斜边中线长是24. 不等式 ＞ +2的解是 ．三、解答题
-
25.
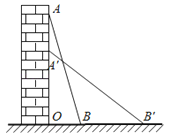
如图所示，一根长2.5米的木棍（AB），斜靠在与地面（OM）垂直的墙（ON）上，此时OB的距离为0.7米，设木棍的中点为P．若木棍A端沿墙下滑，且B端沿地面向右滑行．
（1）如果木棍的顶端A沿墙下滑0.4米，那么木棍的底端B向外移动多少距离？
（2）请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由．
26. 判断以下各题的结论是否正确（对的打“√”，错的打“×”）．（1）若 b﹣3a＜0，则b＜3a；
（2）如果﹣5x＞20，那么x＞﹣4；
（3）若a＞b，则 ac2＞bc2；
（4）若ac2＞bc2 ， 则a＞b；
（5）若a＞b，则 a（c2+1）＞b（c2+1）．
（6）若a＞b＞0，则＜ ．
27.如图，圆柱的高为8cm，底面半径为2cm，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面上与A点相对的B点处的食物，它需要爬行的最短路程是多少厘米？（圆周率取3）
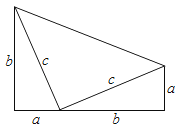
28.教材在探索平方差公式时利用了面积法，面积法除了可以帮助我们记忆公式，还可以直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为a，较小的直角边长都为b，斜边长都为c），大正方形的面积可以表示为c2 ， 也可以表示为4×ab+(a-b)2由此推导出重要的勾股定理：如果直角三角形两条直角边长为a，b，斜边长为c，则a2+b2=c2 ．
（1）图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．
（2）如图③，直角△ABC中，∠ACB=90°，AC=3cm，BC=4cm，则斜边AB上的高CD的长为.
（3）试构造一个图形，使它的面积能够解释（a+b）（a+2b）=a2+3ab+2b2 ， 画在如图4的网格中，并标出字母a、b所表示的线段．
29.勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2
证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC=b2+ab．
又∵S四边形ADCB=S△ADB+S△DCB=c2+a（b﹣a）
∴b2+ab=c2+a（b﹣a）
∴a2+b2=c2
请参照上述证法，利用图2完成下面的证明．
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2 ．
30.如图，在△ABC中，∠C=90°，AB的垂直平分线DE交AC于D，垂足为E，若∠A=30°，CD=3．
（1）求∠BDC的度数．
（2）求AC的长度．
