人教版数学八年级下学期平行四边形单元试卷
试卷更新日期:2018-02-24 类型:单元试卷
一、单选题
-
1. 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )
 A、17 B、18 C、19 D、202. 顺次连结矩形四边中点所得的四边形一定是( )A、菱形 B、矩形 C、正方形 D、等腰梯形3. 如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 .
A、17 B、18 C、19 D、202. 顺次连结矩形四边中点所得的四边形一定是( )A、菱形 B、矩形 C、正方形 D、等腰梯形3. 如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 .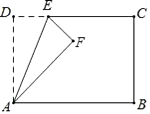 4. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
4. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )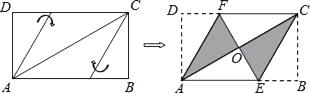 A、1 B、 C、 D、45. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
A、1 B、 C、 D、45. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )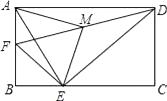 A、5 B、 C、 D、6. 如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值 ﹣1.其中正确的说法有( )个.
A、5 B、 C、 D、6. 如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值 ﹣1.其中正确的说法有( )个.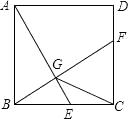 A、4 B、3 C、2 D、17.
A、4 B、3 C、2 D、17.在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA。若∠ACB=21°,则∠ECD的度数是( )
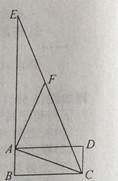 A、7° B、21° C、23° D、24°8. 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )
A、7° B、21° C、23° D、24°8. 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )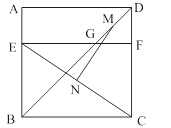 A、3 B、 C、 D、49. 如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A、3 B、 C、 D、49. 如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )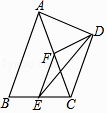 A、∠ECD=112.5° B、DE平分∠FDC C、∠DEC=30° D、AB= CD10. 下列性质中菱形不一定具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、既是轴对称图形又是中心对称图形11. 如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( )
A、∠ECD=112.5° B、DE平分∠FDC C、∠DEC=30° D、AB= CD10. 下列性质中菱形不一定具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、既是轴对称图形又是中心对称图形11. 如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( ) A、BD<2 B、BD=2 C、BD>2 D、以上情况均有可能
A、BD<2 B、BD=2 C、BD>2 D、以上情况均有可能二、综合题
-
12. 如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:
 (1)、△ABF与△ AGF全等吗?说明理由;
(1)、△ABF与△ AGF全等吗?说明理由;
(2)、求∠EAF的度数;(3)、若AG=4,△AEF的面积是7,求△CEF的面积.13. 在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。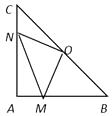 (1)、写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;(2)、如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。14. ABCD中,E是CD边上一点,(1)、将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ .
(1)、写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;(2)、如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。14. ABCD中,E是CD边上一点,(1)、将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ .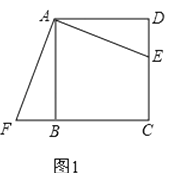 (2)、如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ.
(2)、如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ.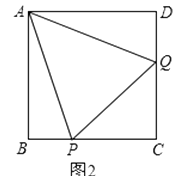 (3)、在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2 .
(3)、在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2 .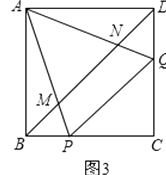 15. 如图,在长方形 中, , ,点 从点 出发,以 的速度沿 向点 运动,设点 的运动时间为 秒:
15. 如图,在长方形 中, , ,点 从点 出发,以 的速度沿 向点 运动,设点 的运动时间为 秒: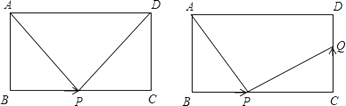
(1)、 .(用 的代数式表示)(2)、当 为何值时,(3)、当点 从点 开始运动,同时,点 从点 出发,以 v 的速度沿 向点 运动,是否存在这样的v 值,使得 全等?若存在,请求出 v的值;若不存在,请说明理由.
16. 如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D. (1)、当AC的长度为多少时,△AMC和△BOD相似;(2)、当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;(3)、连结BC.当S△AMC=S△BOC时,求AC的长.17. 在边长为2的正方形ABCD中,点P、Q分别是边AB、BC上的两个动点(与点A、B、C不重合),且始终保持BP=BQ,AQ⊥QE,QE交正方形外角平分线CE于点E,AE交CD于点F,连结PQ.
(1)、当AC的长度为多少时,△AMC和△BOD相似;(2)、当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;(3)、连结BC.当S△AMC=S△BOC时,求AC的长.17. 在边长为2的正方形ABCD中,点P、Q分别是边AB、BC上的两个动点(与点A、B、C不重合),且始终保持BP=BQ,AQ⊥QE,QE交正方形外角平分线CE于点E,AE交CD于点F,连结PQ.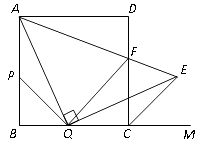 (1)、求证:△APQ≌△QCE;(2)、求∠QAE的度数;(3)、设BQ=x,当x为何值时,QF∥CE,并求出此时△AQF的面积.18. 已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上,AH=2.(1)、如图1,当DG=2,且点F在边BC上时.
(1)、求证:△APQ≌△QCE;(2)、求∠QAE的度数;(3)、设BQ=x,当x为何值时,QF∥CE,并求出此时△AQF的面积.18. 已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上,AH=2.(1)、如图1,当DG=2,且点F在边BC上时.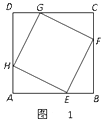
求证:① △AHE≌△DGH;
② 菱形EFGH是正方形;
(2)、如图2,当点F在正方形ABCD的外部时,连接CF.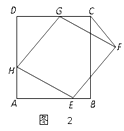
① 探究:点F到直线CD的距离是否发生变化?并说明理由;
② 设DG=x,△FCG的面积为S,是否存在x的值,使得S=1,若存在,求出x的值;若不存在,请说明理由.
19. 在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= AD,点N是折线AB﹣BC上的一个动点.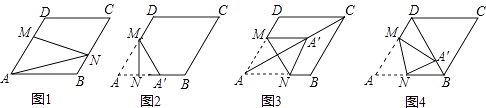 (1)、如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .(2)、当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
(1)、如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .(2)、当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,①若点A′落在AB边上,则线段AN的长度为;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 的值.
20. 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.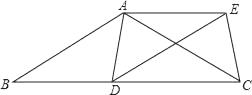 (1)、求证:△ADC≌△ECD;
(1)、求证:△ADC≌△ECD;
(2)、当点D在什么位置时,四边形ADCE是矩形,请说明理由.
21. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE= AC,连接AE交OD于点F,连接CE、OE.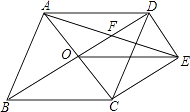 (1)、求证:OE=CD;(2)、若菱形ABCD的边长为2,∠ABC=60°,求AE的长.22. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
(1)、求证:OE=CD;(2)、若菱形ABCD的边长为2,∠ABC=60°,求AE的长.22. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.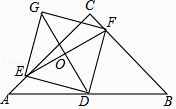 (1)、求证:四边形EDFG是正方形;(2)、当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.23. 如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)、求证:四边形EDFG是正方形;(2)、当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.23. 如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.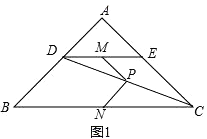 (1)、观察猜想
(1)、观察猜想图1中,线段PM与PN的数量关系是 , 位置关系是;
(2)、探究证明把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
 (3)、拓展延伸
(3)、拓展延伸把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
三、填空题
-
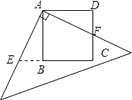
24. 有一块边长为4的正方形ABCD,将一块足够大的直角三角板如图放置, CB延长线与直角边交于点E.则四边形AECF的面积是 .
 25. 如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 .
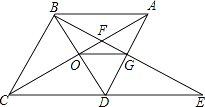
25. 如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 .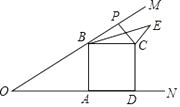 26. 如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上)
26. 如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上)①OG= AB;
②与△EGD全等的三角形共有5个;
③S四边形CDGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
四、解答题
-
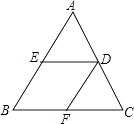
27. 如图,已知菱形BEDF,内接于△ABC,点E,D,F分别在AB,AC和BC上.若AB=15cm,BC=12cm,求菱形边长.
 28.
28.如图, 是 的中线, 是线段 上一点(不与点 重合). 交 于点 , ,连结 .
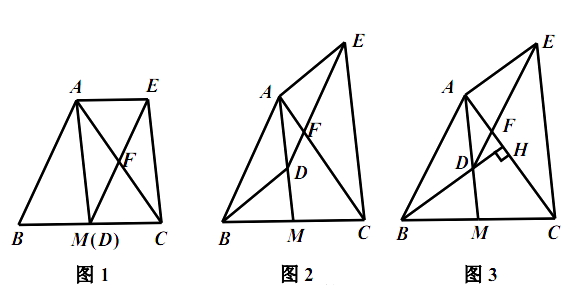 (1)、如图1,当点 与 重合时,求证:四边形 是平行四边形;(2)、如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.(3)、如图3,延长 交 于点 ,若 ,且 .
(1)、如图1,当点 与 重合时,求证:四边形 是平行四边形;(2)、如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.(3)、如图3,延长 交 于点 ,若 ,且 .①求 的度数;
②当 , 时,求 的长.
29.已知正方形 的对角线 , 相交于点 .
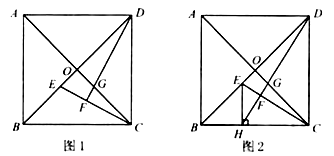 (1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,
(1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,①求证: ;
②当 时,求 的长.
30.如图1,已知▱ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是▱ABCD边上的一个动点.

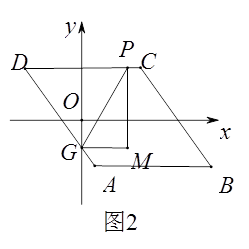 (1)、若点P在边BC上,PD=CD,求点P的坐标.(2)、若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)、若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
(1)、若点P在边BC上,PD=CD,求点P的坐标.(2)、若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)、若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).