人教版数学八年级下学期勾股定理单元试卷
试卷更新日期：2018-02-24 类型：单元试卷
一、单选题
-
1. 如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD长（ ）
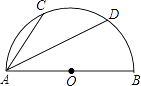A、4 cm B、3 cm C、5 cm D、4 cm2. 如图，在△ABC中，BC=10，∠B=60°，∠C=45°，则点A到BC的距离是（ ）
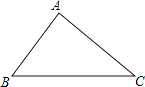A、10﹣5 B、5+5 C、15﹣5 D、15﹣103. 如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段DE的长为（ ）.
A、3 B、 C、5 D、4. 如图，在矩形ABCD中，AB=4，AD=6，点F是AB的中点，E为BC边上一点，且EF⊥ED，连结DF，M为DF的中点，连结MA，ME．若AM⊥ME，则AE的长为（ ）
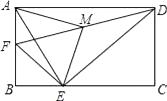A、5 B、 C、 D、5. 如图，已知正方形ABCD的边长为2，E是边BC上的动点，BF⊥AE交CD于点F，垂足为点G，连接CG，下列说法：①AG＞GE；②AE=BF；③点G运动的路径长为π；④CG的最小值 ﹣1．其中正确的说法有（ ）个．
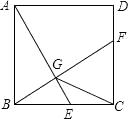A、4 B、3 C、2 D、16.如图，四边形ABCD是边长为6的正方形，点E在边AB上，BE＝4，过点E作EF∥BC，分别交BD、CD于G、F两点．若M、N分别是DG、CE的中点，则MN的长为 （ ）
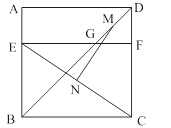A、3 B、 C、 D、47. 如图，△ABC中，E为BC边的中点，CD⊥AB，AB=2，AC=1，DE= ，则∠CDE+∠ACD=（ ）
A、60° B、75° C、90° D、105°8.四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH．已知AM为Rt△ABM较长直角边，AM=2 EF，则正方形ABCD的面积为（ ）
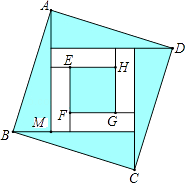A、12S B、10S C、9S D、8S9. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（ ）
A、 B、 C、 D、二、综合题
-
10. 如图，A（-5，0），B（-3，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB．∠CDA=90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时时间t秒．
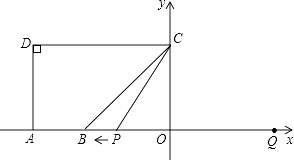(1)、求点C的坐标；(2)、当∠BCP=15°时，求t的值；(3)、以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值．
11. 在图1﹣﹣图4中，菱形ABCD的边长为3，∠A=60°，点M是AD边上一点，且DM= AD，点N是折线AB﹣BC上的一个动点．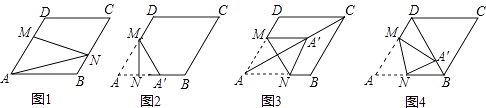
(1)、如图1，当N在BC边上，且MN过对角线AC与BD的交点时，则线段AN的长度为 ．(2)、当点N在AB边上时，将△AMN沿MN翻折得到△A′MN，如图2，①若点A′落在AB边上，则线段AN的长度为；
②当点A′落在对角线AC上时，如图3，求证：四边形AM A′N是菱形；
③当点A′落在对角线BD上时，如图4，求 的值．
12. 根据所学知识完成小题：(1)、如图1，锐角△ABC中，分别以AB、AC为边向外作等边△ABE和等边△ACD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．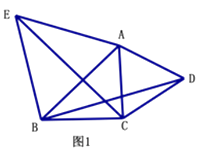
(2)、【深入探究】如图2，△ABC中，∠ABC=45°，AB=5cm，BC=3cm，分别以AB、AC为边向外作正方形ABNE和正方形ACMD，连接BD，求BD的长．
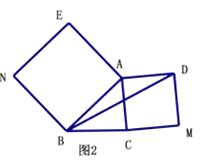(3)、如图3，在（2）的条件下，以AC为直角边在线段AC的左侧作等腰直角△ACD，求BD的长．
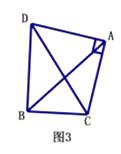13. 在四边形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm，点P从点A出发，沿折线ABCD方向以3cm/s的速度匀速运动；点Q从点D出发，沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发，当一个点到达终点时，另一点也停止运动，设运动时间为t（s）.
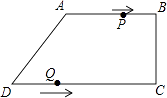(1)、求CD的长；(2)、当四边形PBQD为平行四边形时，求四边形PBQD的周长；(3)、在点P、Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在，请求出所有满足条件的t的值；若不存在，请说明理由.14. 如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC．
(1)、求证：CD=AN；(2)、若AC⊥DN，∠CAN=30°，MN=1，求四边形ADCN的面积．15. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC且DE= AC，连接AE交OD于点F，连接CE、OE．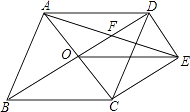
(1)、求证：OE=CD；(2)、若菱形ABCD的边长为2，∠ABC=60°，求AE的长．16. 如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．
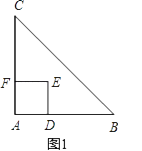(1)、当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．
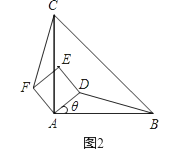(2)、当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．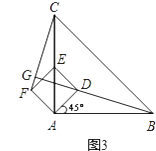
①求证：BD⊥CF；
②当AB=4，AD= 时，求线段BG的长．
17.如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．
(1)、写出线段AG，GE，GF长度之间的数量关系，并说明理由；(2)、若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．
18.如图，在△ABC中，点O是边AC上一个动点，过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．
(1)、若CE=8，CF=6，求OC的长；(2)、连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．
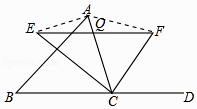19. 我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2 ．(1)、在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC= ， OC△OA=；
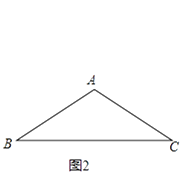
(2)、如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；
(3)、如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON= AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．
20.如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=30°．
(1)、求证：△ABD∽△DCE；(2)、设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围；(3)、当△ADE是等腰三角形时，求AE的长．21.如图，矩形ABCD的对角线AC，BD相交于点O，△COD关于CD的对称图形为△CED．
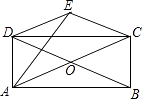(1)、求证：四边形OCED是菱形；(2)、连接AE，若AB=6cm，BC= cm．①求sin∠EAD的值；
②若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，再以1.5cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动，当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间．
三、填空题
-
22. 一等腰三角形的两边长分别为4cm和6cm，则其底角的余弦值为 ．23.
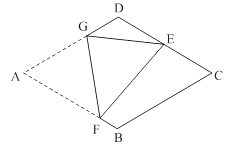
如图，在菱形纸片ABCD中，AB＝2，∠A＝60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上．则cos∠EFG的值为 ．
24. 如图，△ABC中，AC=5，BC=12，AB=13，CD是AB边上的中线．则CD= ．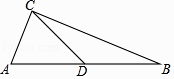
25.如图，在Rt△ABC中，∠BAC=90°，AB=15，AC=20，点D在边AC上，AD=5，DE⊥BC于点E，连结AE，则△ABE的面积等于 ．
26.如图，已知菱形ABCD的周长为16，面积为8 ，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为 ．
27. 如图，在△ABC中，∠ACB=90°，点D，E分别在AC，BC上，且∠CDE=∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC=8，AB=10，则CD的长为 ．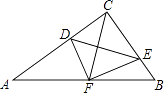
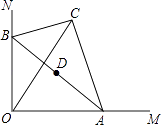
28.如图，在Rt△ABC中，BC=2，∠BAC=30°，斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动，下列结论：
①若C、O两点关于AB对称，则OA=2 ；
②C、O两点距离的最大值为4；
③若AB平分CO，则AB⊥CO；
④斜边AB的中点D运动路径的长为 ；
其中正确的是（把你认为正确结论的序号都填上）．
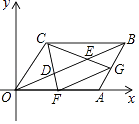
29.如图，平面直角坐标系中O是原点，▱ABCD的顶点A，C的坐标分别是（8，0），（3，4），点D，E把线段OB三等分，延长CD、CE分别交OA、AB于点F，G，连接FG．则下列结论：
①F是OA的中点；②△OFD与△BEG相似；③四边形DEGF的面积是 ；④OD=
其中正确的结论是（填写所有正确结论的序号）．
四、解答题
-
30.
在一次课题学习中，老师让同学们合作编题．某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解．
如图，将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H，使得AE＝CG，BF＝DH，连结EF、FG、GH、HE．
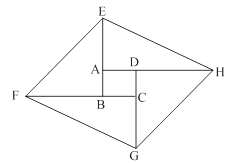(1)、求证：四边形EFGH为平行四边形；(2)、若矩形ABCD是边长为1的正方形，且∠FEB＝45°，tan∠AEH＝2，求AE的长．