2015-2016学年江西省赣州市石城县八年级下学期期中数学试卷
试卷更新日期:2016-11-10 类型:期中考试
一、选择题
-
1. 二次根式化为最简二次根式是( )A、 B、 C、 D、2. 如图,矩形ABCD中,AB<BC,对角线AC、BD相交于点O,则图中的等腰三角形有( )
 A、2个 B、4个 C、6个 D、8个3. 计算( ﹣ )÷ 的结果是( )A、﹣1 B、﹣ C、 D、14. 下列各组数据中的是三个数作为三角形的边长,其中能构成直角三角形的是( )A、1, , B、 , , C、5,6,7 D、7,8,95. 如图,在▱ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
A、2个 B、4个 C、6个 D、8个3. 计算( ﹣ )÷ 的结果是( )A、﹣1 B、﹣ C、 D、14. 下列各组数据中的是三个数作为三角形的边长,其中能构成直角三角形的是( )A、1, , B、 , , C、5,6,7 D、7,8,95. 如图,在▱ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( ) A、BO=DO B、CD=AB C、∠BAD=∠BCD D、AC=BD6. 如图中,边长k等于5的直角三角形有( )
A、BO=DO B、CD=AB C、∠BAD=∠BCD D、AC=BD6. 如图中,边长k等于5的直角三角形有( ) A、1个 B、2个 C、3个 D、4个7. 已知四边形ABCD,下列说法正确的是( )A、当AD=BC,AB∥DC时,四边形ABCD是平行四边形 B、当AD=BC,AB=DC时,四边形ABCD是平行四边形 C、当AC=BD,AC平分BD时,四边形ABCD是矩形 D、当AC=BD,AC⊥BD时,四边形ABCD是正方形8. 如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A、1个 B、2个 C、3个 D、4个7. 已知四边形ABCD,下列说法正确的是( )A、当AD=BC,AB∥DC时,四边形ABCD是平行四边形 B、当AD=BC,AB=DC时,四边形ABCD是平行四边形 C、当AC=BD,AC平分BD时,四边形ABCD是矩形 D、当AC=BD,AC⊥BD时,四边形ABCD是正方形8. 如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( ) A、﹣4和﹣3之间 B、3和4之间 C、﹣5和﹣4之间 D、4和5之间9. 如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为( )
A、﹣4和﹣3之间 B、3和4之间 C、﹣5和﹣4之间 D、4和5之间9. 如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为( ) A、16a B、12a C、8a D、4a10. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A、16a B、12a C、8a D、4a10. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )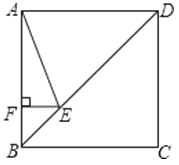 A、1 B、 C、4﹣2 D、3﹣4
A、1 B、 C、4﹣2 D、3﹣4二、填空题
-
11. 若 =2,则a= .12. 如图,在Rt△ABC中,∠ACB=90°,AB=20cm,点D为AB的中点,则CD=cm.
 13. 如图,以△ABC的两边BC、AC分别向外作正方形,它们的面积分别是S1 , S2 , 若S1=2,S2=3,AB2=5,则△ABC的形状是三角形.
13. 如图,以△ABC的两边BC、AC分别向外作正方形,它们的面积分别是S1 , S2 , 若S1=2,S2=3,AB2=5,则△ABC的形状是三角形. 14. 在平面直角坐标系中,点A的坐标为A( ,﹣2 ),先将点A向上平移3 个单位长度,再向左平移2 个单位长度得到点A′,则点A′的坐标是 .15. 如图,点E在正方形ABCD的边CD上,若△ABE的面积为32,CE=6,则线段BE的长为 .
14. 在平面直角坐标系中,点A的坐标为A( ,﹣2 ),先将点A向上平移3 个单位长度,再向左平移2 个单位长度得到点A′,则点A′的坐标是 .15. 如图,点E在正方形ABCD的边CD上,若△ABE的面积为32,CE=6,则线段BE的长为 . 16. 如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .
16. 如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .
三、解答题
-
17. 计算: .18.
我们把能二等分多边形面积的直线称为多边形的“好线”,请用无刻度的直尺作出图(1)、图(2)的“好线”.其中图(1)是一个平行四边形,图(2)由一个平行四边形和一个正方形组成.(保留作图痕迹,不写作法)
 19. 已知x= -1,y= +1,求 的值.20. 如图:在平行四边形ABCD中,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:CF=EF.
19. 已知x= -1,y= +1,求 的值.20. 如图:在平行四边形ABCD中,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证:CF=EF. 21. 如图,已知△ABC,按如下步骤作图:
21. 如图,已知△ABC,按如下步骤作图:
①分别以A、C为圆心,以大于 AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)、求证:四边形ADCE是菱形;(2)、当∠ACB=90°,BC=6,△ADC的周长为18时,求四边形ADCE的面积.22. 小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,A、B、D三点在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8. (1)、试求点F到AD的距离.(2)、试求BD的长.23. 如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)、试求点F到AD的距离.(2)、试求BD的长.23. 如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N. (1)、请你判断OM和ON的数量关系,并说明理由;(2)、过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.24. 如图1,矩形纸片ABCD的边长AB=4cm,AD=2cm.同学小明现将该矩形纸片沿EF折痕,使点A与点C重合,折痕后在其一面着色(如图2),观察图形对比前后变化,回答下列问题:
(1)、请你判断OM和ON的数量关系,并说明理由;(2)、过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.24. 如图1,矩形纸片ABCD的边长AB=4cm,AD=2cm.同学小明现将该矩形纸片沿EF折痕,使点A与点C重合,折痕后在其一面着色(如图2),观察图形对比前后变化,回答下列问题: (1)、GFFD:(直接填写=、>、<)(2)、判断△CEF的形状,并说明理由;(3)、小明通过此操作有以下两个结论:
(1)、GFFD:(直接填写=、>、<)(2)、判断△CEF的形状,并说明理由;(3)、小明通过此操作有以下两个结论:①四边形EBCF的面积为4cm2
②整个着色部分的面积为5.5cm2
运用所学知识,请论证小明的结论是否正确.
25.如图①,在正方形ABCD中,E是线段AB上一动点,点F在AD的延长线上运动,且DF=BE.
 (1)、求证:CE=CF.(2)、当点E在AB上运动时,在AD上取一点G,使∠GCE=45°,试判断BE、EG、GD三条线段的数量关系,并加以证明.(3)、若连接图①中的BD,分别交CE、CG于点M、N,得图②,试根据(2)中的结论说明以线段BM、MN、DN为三边构成的是一个什么形状的三角形?
(1)、求证:CE=CF.(2)、当点E在AB上运动时,在AD上取一点G,使∠GCE=45°,试判断BE、EG、GD三条线段的数量关系,并加以证明.(3)、若连接图①中的BD,分别交CE、CG于点M、N,得图②,试根据(2)中的结论说明以线段BM、MN、DN为三边构成的是一个什么形状的三角形?