2015-2016学年湖北省宜昌五中八年级上学期期中数学试卷

试卷更新日期：2016-11-10 类型：期中考试

进入 出卷网 下载

一、选择题

  • 1. 一个多边形的内角和是外角和的2倍，则这个多边形是（  ）
    A、四边形 B、五边形 C、六边形 D、八边形

    查看试题解析

  • 2. 张明的父母打算购买一种形状和大小都相同的正多边形瓷砖来铺地板，为了保证铺地板时既没缝隙，又不重叠，则所购瓷砖形状不能是（　　）

    A、正三角形 B、正方形 C、正六边形 D、正八边形

    查看试题解析

  • 3.

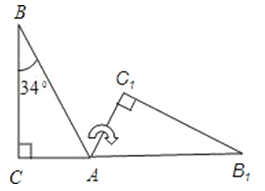
    如图，将Rt△ABC（其中∠B=34°，∠C=90°）绕A点按顺时针方向旋转到△AB1C1的位置，使得点C，A，B1在同一条直线上，那么旋转角最小等于（　　）

     

    A、56° B、68°   C、124° D、180°

    查看试题解析

  • 4. 若三角形两边的长分别为7cm和2cm，第三边为奇数，则第三边的长为（  ）
    A、3 B、5 C、7 D、9

    查看试题解析

  • 5. 能使两个直角三角形全等的条件是（　　）

    A、斜边相等 B、两直角边对应相等 C、两锐角对应相等 D、一锐角对应相等

    查看试题解析

  • 6. 点P（2，﹣3）关于x轴的对称点是（  ）
    A、（﹣2，3） B、（2，3） C、（﹣2，-3） D、（2，﹣3）

    查看试题解析

  • 7. 已知：△ABC中，AB=AC=x，BC=6，则腰长x的取值范围是（  ）

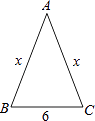    A、0＜x＜3 B、x＞3 C、3＜x＜6 D、x＞6

    查看试题解析

  • 8. 如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为（  ）

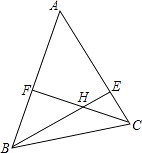    A、160° B、150° C、140° D、130°

    查看试题解析

  • 9. 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=35°，那么∠2是（  ）°．

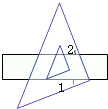    A、55 B、35 C、65 D、25

    查看试题解析

  • 10. 如图，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA=PB，下列确定P点的方法正确的是（  ）

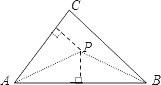    A、P是∠A与∠B两角平分线的交点 B、P为∠A的角平分线与AB的垂直平分线的交点 C、 P为AC、AB两边上的高的交点 D、P为AC、AB两边的垂直平分线的交点

    查看试题解析

  • 11. 小亮在镜中看到身后墙上的时钟如下，你认为实际时间最接近8：00的是（  ）

    A、 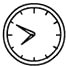B、 C、 D、

    查看试题解析

  • 12. 如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（  ）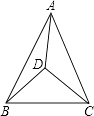

    A、100° B、80° C、70° D、50°

    查看试题解析

  • 13. 在等腰△ABC中，AB=AC=9，BC=6，DE是AC的垂直平分线，交AB、AC于点D、E，则△BDC的周长是（  ）

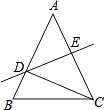    A、6 B、9 C、12 D、15

    查看试题解析

  • 14. 一根直尺EF压在三角板30°的角∠BAC上，与两边AC，AB交于M、N．那么∠CME+∠BNF是（  ）

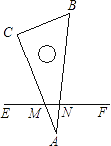    A、150° B、180° C、135° D、不能确定

    查看试题解析

  • 15. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，DF⊥AC交AC于点F．S△ABC=7，DE=2，AB=4，则AC长是（  ）

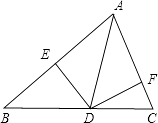    A、4 B、3 C、6 D、5

    查看试题解析

二、解答题

  • 16. 已知：如图，AB∥ED，点F、点C在AD上，AB=DE，AF=DC．求证：BC=EF．

    查看试题解析

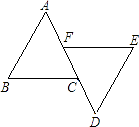  • 17. 如图，已知DE∥BC，CD是∠ACB的平分线，∠B=70°，∠ACB=50°，求∠EDC和∠BDC的度数．

    查看试题解析

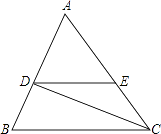  • 18. 如图所示，AD，AE是三角形ABC的高和角平分线，∠B=36°，∠C=76°，求∠DAE的度数．

    查看试题解析

  • 19. 如图，有一长方形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，求△CEF的面积．

    查看试题解析

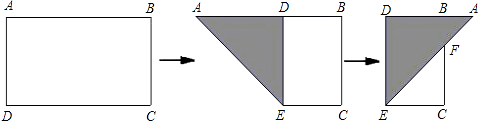  • 20. 如图，在△ABD和△ACD中，已知AB=AC，∠B=∠C，求证：AD是∠BAC的平分线．

    查看试题解析

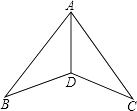  • 21. 如图，在△ABC中，D为BC的中点，DE⊥BC交∠BAC的平分线AE于E，EF⊥AB于F，EG⊥AC交AC延长线于G．求证：BF=CG．

    查看试题解析

  • 22. 如图，已知锐角△ABC中，AB、AC边的中垂线交于点O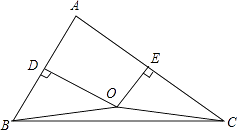

    (1)、若∠A=α（0°＜α＜90°），求∠BOC；
    (2)、试判断∠ABO+∠ACB是否为定值；若是，求出定值，若不是，请说明理由．

    查看试题解析

  • 23. 某公司有2位股东，20名工人、从2006年至2008年，公司每年股东的总利润和每年工人的工资总额如图所示．

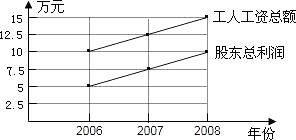    (1)、填写下表：

    年份

    2006年

    2007年

    2008年

    工人的平均工资/元

    5000



    股东的平均利润/元

    25000



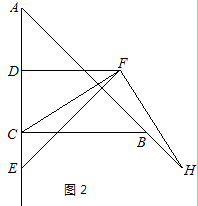
    (2)、假设在以后的若干年中，每年工人的工资和股东的利润都按上图中的速度增长，那么到哪一年，股东的平均利润是工人的平均工资的8倍？

    查看试题解析

  • 24. 在△ABC中，AC=BC，∠ACB=90°，点D为AC的中点．
    (1)、如图1，E为线段DC上任意一点，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，过点F作FH⊥FC，交直线AB于点H．判断FH与FC的数量关系并加以证明；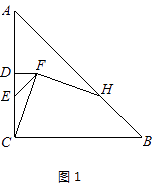

    (2)、如图2，若E为线段DC的延长线上任意一点，（1）中的其他条件不变，你在（1）中得出的结论是否发生改变，直接写出你的结论，不必证明．

    查看试题解析