2015-2016学年湖北省宜昌二十五中八年级上学期期中数学试卷
试卷更新日期:2016-11-10 类型:期中考试
一、选择题
-
1. 下列长度的各种线段,可以组成三角形的是( )A、2,3,4 B、1,1,2 C、4,4,9 D、7,5,12. 从五边形的一个顶点作对角线,把这个五边形分成三角形的个数是( )A、5个 B、4个 C、3个 D、2个3. 在△ABC中,∠A=2∠B=75°,则∠C等于( )A、30° B、67.5° C、105° D、135°4. 如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
 A、∠A=∠B B、AO=BO C、AB=CD D、AC=BD5. 下列图形中有稳定性的是( )A、正方形 B、长方形 C、直角三角形 D、平行四边形6. 若一个多边形的内角和为1080°,则这个多边形的边数为( )A、6 B、7 C、8 D、97. 若一个多边形的每个外角都为30°,则这个多边形是( )A、十二边形 B、十边形 C、八边形 D、六边形8. 等腰三角形的两边长分别为3和6,那么该三角形的周长为( )A、12 B、15 C、10 D、12或159. 下列从左到右的变形是因式分解的是( )A、(﹣a+b)2=a2﹣2ab+b2 B、m2﹣4m+3=(m﹣2)2﹣1 C、﹣a2+9b2=﹣(a+3b)(a﹣3b) D、(x﹣y)2=(x+y)2﹣4xy10. 若3x=15,3y=5,则3x﹣y等于( )A、5 B、3 C、15 D、1011. 下列各式是完全平方式的是( )A、x2﹣x+ B、1+x2 C、x+xy+1 D、x2+2x﹣112. 下列说法正确的是( )A、三个角对应相等的两个三角形全等 B、面积相等的两个三角形全等 C、全等三角形的面积相等 D、两边和其中一边的对角对应相等的两个三角形全等13. 如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
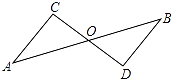
A、∠A=∠B B、AO=BO C、AB=CD D、AC=BD5. 下列图形中有稳定性的是( )A、正方形 B、长方形 C、直角三角形 D、平行四边形6. 若一个多边形的内角和为1080°,则这个多边形的边数为( )A、6 B、7 C、8 D、97. 若一个多边形的每个外角都为30°,则这个多边形是( )A、十二边形 B、十边形 C、八边形 D、六边形8. 等腰三角形的两边长分别为3和6,那么该三角形的周长为( )A、12 B、15 C、10 D、12或159. 下列从左到右的变形是因式分解的是( )A、(﹣a+b)2=a2﹣2ab+b2 B、m2﹣4m+3=(m﹣2)2﹣1 C、﹣a2+9b2=﹣(a+3b)(a﹣3b) D、(x﹣y)2=(x+y)2﹣4xy10. 若3x=15,3y=5,则3x﹣y等于( )A、5 B、3 C、15 D、1011. 下列各式是完全平方式的是( )A、x2﹣x+ B、1+x2 C、x+xy+1 D、x2+2x﹣112. 下列说法正确的是( )A、三个角对应相等的两个三角形全等 B、面积相等的两个三角形全等 C、全等三角形的面积相等 D、两边和其中一边的对角对应相等的两个三角形全等13. 如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )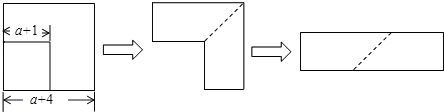 A、(2a2+5a)cm2 B、(3a+15)cm2 C、(6a+15)cm2 D、(8a+15)cm214. 如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( )对.
A、(2a2+5a)cm2 B、(3a+15)cm2 C、(6a+15)cm2 D、(8a+15)cm214. 如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( )对.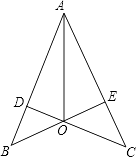 A、2 B、3 C、4 D、515. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F.S△ABC=7,DE=2,AB=4,则AC长是( )
A、2 B、3 C、4 D、515. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F.S△ABC=7,DE=2,AB=4,则AC长是( )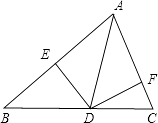 A、4 B、3 C、6 D、5
A、4 B、3 C、6 D、5二、解答题
-
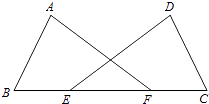
16. 计算题(ab2)2•(﹣a3b)3÷(﹣5ab)17. 如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
 18. 先化简,再求值:2(x﹣3)(x+2)﹣(3+a)(3﹣a),其中a=﹣2,x=1.19. 如图,已知FD⊥BC于D,DE⊥AB于E,∠B=∠C,∠AFD=140°,求∠EDF的度数.
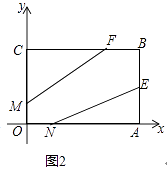
18. 先化简,再求值:2(x﹣3)(x+2)﹣(3+a)(3﹣a),其中a=﹣2,x=1.19. 如图,已知FD⊥BC于D,DE⊥AB于E,∠B=∠C,∠AFD=140°,求∠EDF的度数.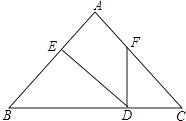 20. 如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m﹣3)2+n2﹣6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.
20. 如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m﹣3)2+n2﹣6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点. (1)、求m、n的值并写出A、B、C三点的坐标;(2)、若OF+BE=AB,求证:CF=CE.21. 如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G.求证:
(1)、求m、n的值并写出A、B、C三点的坐标;(2)、若OF+BE=AB,求证:CF=CE.21. 如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G.求证: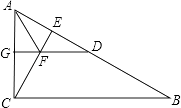 (1)、DF∥BC;(2)、FG=FE.22. 如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿射线AB,BC运动,且它们的速度都为2cm/s.设点P的运动时间为t(s).
(1)、DF∥BC;(2)、FG=FE.22. 如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿射线AB,BC运动,且它们的速度都为2cm/s.设点P的运动时间为t(s).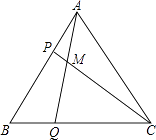 (1)、当t为何值时,△ABQ≌△CBP.(2)、连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.23. 如图,正方形ABCD中,点G是边CD上一点(不与端点C,D重合),以CG为边在正方形ABCD外作正方形CEFG,且B、C、E三点在同一直线上,设正方形ABCD和正方形CEFG的边长分别为a和b.
(1)、当t为何值时,△ABQ≌△CBP.(2)、连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.23. 如图,正方形ABCD中,点G是边CD上一点(不与端点C,D重合),以CG为边在正方形ABCD外作正方形CEFG,且B、C、E三点在同一直线上,设正方形ABCD和正方形CEFG的边长分别为a和b.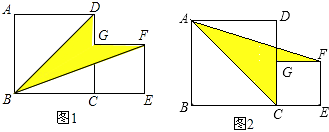 (1)、分别用含a,b的代数式表示图1和图2中阴影部分的面积S1、S2;(2)、如果a+b=5,ab=3,求S1的值;(3)、当S1<S2时,求 的取值范围.24. 在平面直角坐标系中B(3,2),BC⊥y轴于C,BA⊥x轴于A,点E在线段AB上从B向A以每秒1个单位的速度运动,运动时间为t秒(0<t<2).将BE沿BD折叠,使E点恰好落在BC上的F处.
(1)、分别用含a,b的代数式表示图1和图2中阴影部分的面积S1、S2;(2)、如果a+b=5,ab=3,求S1的值;(3)、当S1<S2时,求 的取值范围.24. 在平面直角坐标系中B(3,2),BC⊥y轴于C,BA⊥x轴于A,点E在线段AB上从B向A以每秒1个单位的速度运动,运动时间为t秒(0<t<2).将BE沿BD折叠,使E点恰好落在BC上的F处.
(1)、如图1,若E为AB的中点,请直接写出F、D两点的坐标:F( , ) D( , )(2)、如图1,连接CD,在(1)的条件下,求证:CD=FD.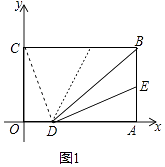 (3)、如图2,在E点运动的同时,M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位.在运动过程中,△CMF能与△ANE全等吗?若能,求出此时a与t的值,若不能,请说明理由.
(3)、如图2,在E点运动的同时,M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位.在运动过程中,△CMF能与△ANE全等吗?若能,求出此时a与t的值,若不能,请说明理由.