2015-2016学年湖北省孝感市云梦县八年级下学期期中数学试卷

试卷更新日期：2016-11-10 类型：期中考试

进入出卷网下载

一、选择题

1. 式子 $\frac{1}{\sqrt{x - 1}}$ 在实数范围内有意义，则x的取值范围是（）

A、x＜1 B、x≤1 C、x＞1 D、x≥1

查看试题解析
2. 计算 $\sqrt{{(- π)}^{2}}$ 的结果是（）

A、﹣π B、π C、π² D、﹣π²

查看试题解析
3. 下列各组数中，不能构成直角三角形的是（）

A、 $\sqrt{5}$ ， $\sqrt{12}$ ， $\sqrt{13}$ B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、3，4，5 D、6，8，10

查看试题解析
4. 下列各式，计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、3 $\sqrt{3}$ - $\sqrt{3}$ =3 C、2 $\sqrt{5} \times 3 \sqrt{5} = 6 \sqrt{5}$ D、（ $\sqrt{8} - \sqrt{6}$ ）÷ $\sqrt{2}$ =2﹣ $\sqrt{3}$

查看试题解析
5. 下列条件中，不能判定四边形是平行四边形的是（　　）

A、两组对边分别平行 B、一组对边平行，另一组对边相等 C、两组对边分别相等 D、一组对边平行且相等

查看试题解析
6. 如图，在△ABC中，AB=5，AC=12，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为（）

A、10 B、12 C、13 D、17

查看试题解析
7. 在四边形ABCD中，对角线AC，BD互相平分，若添加一个条件使得四边形ABCD是菱形，则这个条件可以是（　　）

A、∠ABC=90° B、AC⊥BD C、AB=CD D、AB∥CD

查看试题解析
8. 如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（）

A、12≤a≤13 B、12≤a≤15 C、5≤a≤12 D、5≤a≤13

查看试题解析
9. 如图，Rt△ABC中，∠B=90°，AB=6，BC=9，将△ABC折叠，使C点与AB的中点D重合，折痕为EF，则线段BF的长为（）

A、 $\frac{5}{2}$ B、 $\frac{9}{2}$ C、4 D、5

查看试题解析
10. 如图，正方形ABCD中，点E在AB上，且BE= $\frac{1}{4}$ AB，点F是BC的中点，点G是DE的中点，延长DF，与AB的延长线交于点H．以下四个结论：
①FG= $\frac{1}{2}$ EH；②△DFE是直角三角形；③FG= $\frac{1}{2}$ DE；④DE=EB+BC．
其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 一个直角三角形的一条直角边是7，斜边比另一条直角边长1，则斜边长是．

查看试题解析
12. 若矩形的对角线长为8，两条对角线的一个夹角为60°，则该矩形的面积为．

查看试题解析
13. 已知x= $\sqrt{5}$ +2，y= $\sqrt{5}$ ﹣2，则x²+2xy+y²的值是．

查看试题解析
14. 如图，以菱形AOBC的顶点O为原点，对角线OC所在直线为x轴建立平面直角坐标系，若OB=5，点C的坐标为（8，0），则点A的坐标为

查看试题解析
15. 若a= $\frac{2015}{\sqrt{2016} - 1}$ ，则（a﹣1）²= ．

查看试题解析
16. 如图，在边长为8的正方形ABCD中，E是AB边上的一点，且AE=6，点Q为对角线AC上的动点，则△BEQ周长的最小值为．

查看试题解析

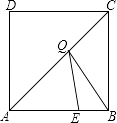
三、解答题

17. 计算：

(1)、（3 $\sqrt{2}$ +2 $\sqrt{3}$ ）²

(2)、（ $\sqrt{48}$ + $\frac{1}{3} \sqrt{6}$ ）÷ $\sqrt{27}$ ．

查看试题解析
18. 观察下列式子：
$\sqrt{2 + \frac{2}{3}}$ =2 $\sqrt{\frac{2}{3}}$ ； $\sqrt{3 + \frac{3}{8}}$ =3 $\sqrt{\frac{3}{8}}$ ； $\sqrt{4 + \frac{4}{15}}$ =4 $\sqrt{\frac{4}{15}}$ ； $\sqrt{5 + \frac{5}{24}}$ =5 $\sqrt{\frac{5}{24}}$
你能看出其中的规律吗？用字母表示这一规律，并给出证明．

查看试题解析
19. 如图，一个长13米的梯子AB斜靠在墙上，这时梯子底端距墙底为5米，如果梯子的顶端沿墙下滑1米，梯子的底端在水平方向也将滑动多少米？（精确到0.01米）

查看试题解析
20. 解答

(1)、已知x= $\sqrt{5}$ +2，求代数式（9﹣4 $\sqrt{5}$ ）x²+（2﹣ $\sqrt{5}$ ）x+ $\sqrt{5}$ 的值．

(2)、先化简，再求值：（a²b+ab）÷ $\frac{a^{2} + 2 a + 1}{a + 1}$ ，其中a= $\sqrt{5}$ +2，b= $\sqrt{5}$ ﹣2．

查看试题解析
21. 如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是40cm．求：

(1)、两条对角线AC、BD的长度；

(2)、菱形ABCD的面积．

查看试题解析
22. 已知等腰三角形ABC的底边长BC=20cm，D是AC上的一点，且BD=16cm，CD=12cm．

(1)、求证：BD⊥AC；

(2)、求△ABC的面积．

查看试题解析
23. 已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，

(1)、求证：四边形ADCE为矩形；

(2)、当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．

查看试题解析
24. 观察探究，解决问题．在四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形．

(1)、
如图1，求证：中点四边形EFGH是平行四边形；

(2)、请你探究并填空：
①当四边形ABCD变成平行四边形时，它的中点四边形是；
②当四边形ABCD变成矩形时，它的中点四边形是；
③当四边形ABCD变成正方形时，它的中点四边形是；

(3)、
如图2，当中点四边形EFGH为矩形时，对角线EG与FH相交于点O，P为EH上的动点，过点P作PM⊥EG，PN⊥FH，垂足分别为M、N，若EF=a，FG=b，请判断PM+PN的长是否为定值？若是，求出此定值；若不是，说明理由．

查看试题解析