2015-2016学年湖北省武汉市江汉区八年级下学期期中数学试卷

试卷更新日期：2016-11-10 类型：期中考试

进入出卷网下载

一、选择题

1. 估算 $\sqrt{7}$ 的值是（　　）

A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2}$ × $\sqrt{3}$ = $\sqrt{6}$ B、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ C、 $\sqrt{8}$ =4 $\sqrt{2}$ D、 $\sqrt{4}$ ﹣ $\sqrt{2}$ = $\sqrt{2}$

查看试题解析
3. 已知矩形一边的长为5，另一边的长为4，则它的对角线的长为（）

A、3 B、 $\sqrt{41}$ C、4 D、2 $\sqrt{41}$

查看试题解析
4. 下列式子中，是最简二次根式的是（）

A、 $\sqrt{\frac{3}{4}}$ B、 $\sqrt{x^{3}}$ C、 $\sqrt{30}$ D、 $\sqrt{27 a}$

查看试题解析
5. 如图，▱ABCD的对角线AC、BD相交于点O，增加下列条件后，▱ABCD不一定是菱形的是（）

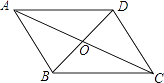A、DC=BC B、AC⊥BD C、AB=BD D、∠ADB=∠CDB

查看试题解析
6. 如图，在边长为2的正方形ABCD中，M为边AD的中点，延长MD至点E，使ME=MC，以DE为边作正方形DEFG，点G在边CD上，则DG的长为（）

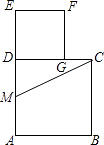A、 $\sqrt{3}$ -1 B、3- $\sqrt{5}$ C、 $\sqrt{5}$ +1 D、 $\sqrt{5}$ -1

查看试题解析
7. 下列说法中，不正确的是（　　）

A、三个角的度数之比为1：3：4的三角形是直角三角形 B、三个角的度数之比为3：4：5的三角形是直角三角形 C、三边长度之比为3：4：5的三角形是直角三角形 D、三边长度之比为9：40：41的三角形是直角三角形

查看试题解析
8. 如图，把菱形ABCD沿AH折叠，使B点落在BC上的E点处，若∠B=70°，则∠EDC的大小为（）

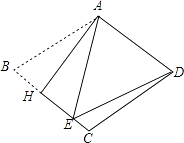A、10° B、15° C、20° D、30°

查看试题解析

二、填空题

9. 化简： $\sqrt{18} - \sqrt{8}$ = ．

查看试题解析
10. 二次根式 $\sqrt{x - 3}$ 在实数范围内有意义的条件是．

查看试题解析
11. 若实数x、y满足 $\sqrt{x - 1}$ + $\sqrt{y + 2}$ =0，则x﹣y的值为．

查看试题解析
12. 在▱ABCD中，∠A：∠B=3：2，则∠D=度．

查看试题解析
13. 若Rt△ABC中，∠C=90°，AC=3，AB=4，则BC=

查看试题解析
14. 矩形的两条对角线的夹角为60°，较短的边长为12cm，则对角线长为 cm．

查看试题解析
15. 菱形ABCD的对角线AC、BD之比为3：4，其周长为40cm，则菱形ABCD的面积为 cm² ．

查看试题解析
16. 下列说法：①平行四边形的一组对边平行且另一组对边相等；②一组对边平行且另一组对边相等的四边形是平行四边形；③菱形的对角线互相垂直；④对角线互相垂直的四边形是菱形，其中正确的说法是（填正确的序号）

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{5 a}$ ×2 $\sqrt{10 b}$

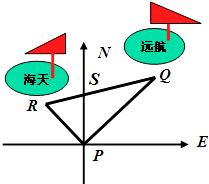
(2)、2b $\sqrt{\frac{a}{b}}$ + $\frac{3}{a} \sqrt{a^{3} b}$ ﹣ $\sqrt{9 a b}$ ．

查看试题解析
18. 某港口位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行？为什么？

查看试题解析
19. 如图，在▱ABCD中，O是对角线AC、BD的交点，BE⊥AC，DF⊥AC，垂足分别为E、F．那么OE与OF是否相等？为什么？

查看试题解析
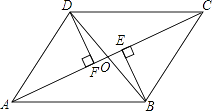20. 如图，四边形ABCD是正方形，△ECF是等腰直角三角形，其中CE=CF，BC=5，CF=3，BF=4．求证：DE∥FC．

查看试题解析
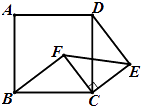21. 如图，已知四边形ABCD中，AD∥BC，∠C=90°，P是CD上一点，BH⊥AP于H，BH=BC=CD

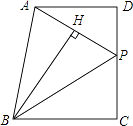(1)、求证：∠ABP=45°；

(2)、若BC=20，PC=12，求AP的长．

查看试题解析

四、选择题

22. 如图，在Rt△ABC中，∠B=90°，AB=3cm，AC=5cm，将△ABC沿DE折叠，使点C与点A重合，则AE的长等于（）

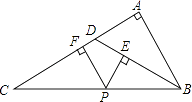
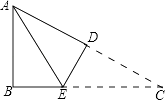A、4cm B、 $\frac{3}{2}$ cm C、 $\frac{25}{8}$ cm D、 $\frac{7}{2}$ cm

查看试题解析
23. 如图所示，△ABC中，∠A=90°，D是AC上一点，且∠ADB=2∠C，P是BC上任一点，PE⊥BD于点E，PE⊥AC于点F，下列结论：
①△DBC是等腰三角形；②∠C=30°；③PE+PF=AB；④PE²+AF²=BP² ．
其中结论正确的序号是（）

A、只有①②③ B、只有①③④ C、只有②④ D、①②③④

查看试题解析

五、填空题

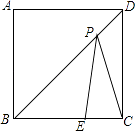
24. 如图，正方形ABCD中，E在BC上，BE=2，CE=1．点P在BD上，则PE与PC的和的最小值为．

查看试题解析
25. 如图，在△ABC中，∠ABC=90°，BD为AC边上的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AG=13，BG=5，则CF的长为．

查看试题解析

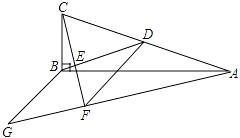
六、解答题

26. 已知△ABC中，∠ACB=90°，D是AB的中点，∠EDF=90°

(1)、如图1，若E、F分别在AC、BC边上，猜想AE²、BF²和EF²之间有何等量关系，并证明你的猜想；

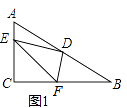(2)、若E、F分别在CA、BC的延长线上，请在图2中画出相应的图形，并判断（1）中的结论是否仍然成立（不作证明）

查看试题解析
27.

(1)、
如图1，点P是▱ABCD内的一点，分别过点B、C、D作AP的垂线BE、CF、DH，垂足分别为E、F、H，猜想BE、CF、DH三者之间的关系，并证明；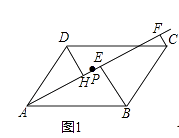

(2)、
如图2，若点P在▱ABCD的外部，△APB的面积为18，△APD的面积为3，求△APC的面积；

(3)、
如图3，在（2）的条件下，增加条件：AB=BC，∠APC=ABC=90°，设AP、BP分别于CD相交于点M、N，当DM=CN时， $\frac{C P}{P M}$ =（请直接写出结论）．

查看试题解析
28. 在平面直角坐标系中，正方形OABC的两边OA、OC分别落在x轴、y轴的正半轴上，等腰Rt△ADE的两个顶点D、E和正方形顶点B三点在一条直线上．

(1)、
如图1，连接OD，求证：△OAD≌△BAE；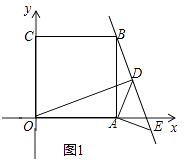

(2)、
如图2，连接CD，求证：BE﹣ $\frac{1}{2}$ DE= $\frac{\sqrt{2}}{2}$ CD；

(3)、
如图3，当图1中的Rt△ADE的顶点D与点B重合时，点E正好落在x轴上，F为线段OC上一动点（不与O、C重合），G为线段AF的中点，若CG⊥GK交BE于点K时，请问∠KCG的大小是否变化？若不变，请求其值；若改变，求出变化的范围．

查看试题解析