2015-2016学年黑龙江省哈尔滨十七中八年级上学期期中数学试卷（五四学制）
试卷更新日期：2016-11-10 类型：期中考试
一、选择题
-
1. 下列运算中，正确的是（ ）A、4a﹣3a=1 B、（ab2）2=a2b2 C、3a6÷a3=3a2 D、a•a2=a32. 下列四个“QQ表情”图片中，不是轴对称图形的是（ ）A、
B、
C、
D、
3. 在直角坐标系中，点P（2，1）关于x轴对称的点的坐标是（ ）A、（2，1） B、（﹣2，1） C、（2，﹣1） D、（﹣2，﹣1）4. 下列各式由左边到右边的变形中，是因式分解的为（ ）A、a（a+1）=a2+a B、a2﹣2a﹣3=a（a﹣2）﹣3 C、（a﹣b）x﹣（a﹣b）y=（a﹣b）（x﹣y） D、（a+b）2﹣4ab=a2﹣2ab+b25. 等腰三角形的一个内角是50°，则其底角是（ ）A、65°或50° B、65° C、50° D、65°或80°6. 代数式9x2+mx+4是个完全平方公式，则m的值为（ ）
A、±6 B、±12 C、±18 D、±97. 与三角形三个顶点距离相等的点，是这个三角形的（ ）A、三条中线的交点 B、三条角平分线的交点 C、三条高的交点 D、三边的垂直平分线的交点8. 已知6m5nx÷2myn3=3m2n2 ， 则（ ）A、x=3，y=2 B、x=5，y=3 C、x=3，y=5 D、x=2，y=39.如图，如图，△ABC中，AB=AC，∠A=30°，且△ABC的面积是4，则AB的长为（ ）
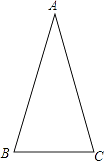A、2 B、4 C、8 D、610.如图，在△ABC中，∠ABC=60°，∠ACB=45°，AD、CF都是高，相交于点P，角平分线BE分别交AD、CF于Q、S，则图中的等腰三角形个数是（ ）
A、2 B、3 C、4 D、5二、填空题
-
11. 光的速度每秒约3×105千米，太阳光射到地球上需要的时间约是5×102秒，则地球与太阳的距离约是千米．12. 若（x﹣5）0=1，则x的取值范围是 ．13. 把多项式x3﹣9x分解因式的结果是 ．14. 计算：（﹣0.5）2015×22015= ．15. 1982=（）2= ．16. 已知：a+b= ， ab=1，式子（a﹣1）（b﹣1）的结果是17. 已知等腰三角形两边长为8cm、4cm．则它的周长是 cm．18.
如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为度．
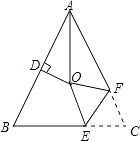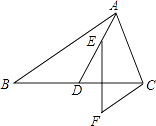
19. △ABC中，BC＞AB＞AC，∠ACB=50°，点D、点E是射线BA上的两个点，且满足AD=AC，BE=BC，则∠DCE的度数为 ．20.如图．在△ABC中，点D在BC边上，BD=DC，点E在AD上，CF∥AB，∠BAD=∠DEF，若AB=5，CF=2．则线段EF的长为 ．
三、解答题
-
21. 先化简，再求值：（x+y）2﹣y（2x+y）﹣8y，其中x=﹣1，y=2．22.
如图，△ABC各顶点坐标是A（﹣3，2）、B（﹣4，﹣3）、C（﹣1，﹣1）．
(1)、画出△ABC关于y轴对称的△A1B1C1；(2)、画出线段AC1和线段CC1 ， 并直接写出△ACC1的面积S的值．23.如图，△ABC是等边三角形，点D、E分别是BC边、AB边上的点，且BE=CD，连接AD、CE交于点F，过A作AH⊥CE于H，
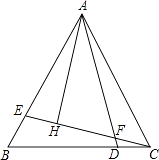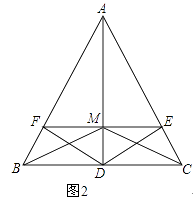
(1)、求证：∠BCE=∠CAD；(2)、直接写出∠CFD的度数；并写出线段AF与线段HF的数量关系．（无需解答过程）24.已知：如图1，点D是△ABC的边BC的中点，DE⊥AC，DF⊥AB，垂足分别为E，F，且BF=CE．
(1)、求证：AE=AF；(2)、如图2，若∠BAC=60°，△ABD的面积为4，连接AD交EF于M，连接BM、CM，在不添加任何辅助线的情况下，请直接写出图中所有面积为1的三角形．
25. 哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育，若购进甲种2株，乙种3株，则共需要成本1700元；若购进甲种3株，乙种1株，则共需要成本1500元．(1)、求甲乙两种君子兰每株成本分别为多少元？(2)、该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰，若购进乙种君子兰的株数比甲种君子兰的3倍还多10株，求最多购进甲种君子兰多少株？26. 如图，△ABD是等腰三角形，AB=AD，将△ABD沿BD翻折得△CBD，点P是线段BD上一点，(1)、如图1，连接PA、PC，求证：CP=AP；
(2)、如图2，连接PA，若∠BAP=90°时，作∠DPF=45°，线段PF交线段CD于F，求证：AD=AP+DF；
(3)、如图3，∠ABD=30°，连接AP并延长交CD于M，若∠BAM=90°，在BD上取一点Q，且DQ=3BQ，连BM、CQ，当BM= 时，求CQ的长．
27.在平面直角坐标系中，点B、A分别在x轴和y轴上，连接AB，已知∠ABO=60°，BC平分∠ABO交y轴于点C，且BC=8．
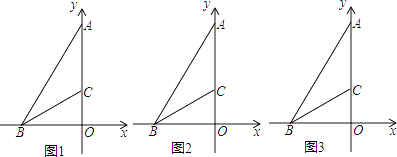(1)、求点A的坐标；(2)、点P从点B出发，沿射线BC方向以每秒2个长度单位的速度运动，过点P作PQ⊥y轴于Q，设点P的运动时间为t秒，试用t表示线段CQ的长；(3)、点D是点B关于y轴的对称点，在（2）的条件下，连接OP、DQ、CD，当 时，求t的值．