2015-2016学年重庆市万州区八年级下学期期末数学试卷
试卷更新日期:2016-11-10 类型:期末考试
一、选择题
-
1. 在 , , ,b+ 中分式的个数有( )A、2个 B、3个 C、4个 D、5个2. 已知函数y= ,自变量x的取值范围是( )A、x≠3且x≠0 B、x>3 C、x<3 D、x≠33. 甲、乙、丙、丁四人进行射击测试,每人10次设计的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
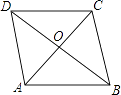 A、4对 B、3对 C、2对 D、1对5. 某校在“中国梦•我的梦”演讲比赛中,有15名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的( )A、平均数 B、众数 C、中位数 D、方差6. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、∠A=∠C,∠B=∠D B、AB∥CD,AB=CD C、AB∥CD,AD∥BC D、AB=CD,AD∥BC7. 如图,▱ABCD的对角线AC、BD相交于点O,增加下列条件后,▱ABCD不一定是菱形的是( )
A、4对 B、3对 C、2对 D、1对5. 某校在“中国梦•我的梦”演讲比赛中,有15名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前8名,不仅要了解自己的成绩,还要了解这15名学生成绩的( )A、平均数 B、众数 C、中位数 D、方差6. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、∠A=∠C,∠B=∠D B、AB∥CD,AB=CD C、AB∥CD,AD∥BC D、AB=CD,AD∥BC7. 如图,▱ABCD的对角线AC、BD相交于点O,增加下列条件后,▱ABCD不一定是菱形的是( )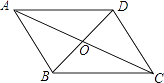 A、DC=BC B、AC⊥BD C、AB=BD D、∠ADB=∠CDB8. 若关于x的方程 ﹣ =0有增根,则m的值是( )A、3 B、4 C、1 D、﹣19. 如图,在正方形ABCD的外侧,作等边△ADE,AC、BE相交于点F,则∠EFC为( )
A、DC=BC B、AC⊥BD C、AB=BD D、∠ADB=∠CDB8. 若关于x的方程 ﹣ =0有增根,则m的值是( )A、3 B、4 C、1 D、﹣19. 如图,在正方形ABCD的外侧,作等边△ADE,AC、BE相交于点F,则∠EFC为( ) A、135° B、145° C、120° D、165°10. 如图,向放在水槽底部的烧杯注水(注水速度不变),注满烧杯后继续注水,直至水槽注满.水槽中水面升上的高度y与注水时间x之间的函数关系,大致是下列图中的( )
A、135° B、145° C、120° D、165°10. 如图,向放在水槽底部的烧杯注水(注水速度不变),注满烧杯后继续注水,直至水槽注满.水槽中水面升上的高度y与注水时间x之间的函数关系,大致是下列图中的( ) A、
A、 B、
B、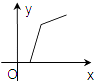 C、
C、 D、
D、 11. 如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
11. 如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( ) A、6 B、2 C、 D、312. 如图,点A是双曲线y= 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A、6 B、2 C、 D、312. 如图,点A是双曲线y= 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( ) A、y= B、y= C、y=﹣ D、y=﹣
A、y= B、y= C、y=﹣ D、y=﹣二、填空题
-
13. 计算:(π﹣3.14)0+|3﹣π|+(﹣ )﹣2= .14. “植树节”时,九年级一班6个小组的植树棵数分别是:5,7,3,x,6,4.已知这组数据的众数是5,则该组数据的平均数是 .15. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 的解是 .
 16. 已知,如图在▱ABCD中,AD=13,AB=10,DE平分∠ADC交BC于点E,则BE= .
16. 已知,如图在▱ABCD中,AD=13,AB=10,DE平分∠ADC交BC于点E,则BE= . 17. 在平面直角坐标系中,直线y=﹣x+2与反比例函数y= 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y= 的图象有2个公共点,则b的取值范围是 .
17. 在平面直角坐标系中,直线y=﹣x+2与反比例函数y= 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y= 的图象有2个公共点,则b的取值范围是 . 18. 如图所示,矩形ABCD的面积为128cm2 , 它的两条对角线交于点O1 , 以AB、AO1为两边邻作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB、AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABC7O7的面积为 .
18. 如图所示,矩形ABCD的面积为128cm2 , 它的两条对角线交于点O1 , 以AB、AO1为两边邻作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB、AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABC7O7的面积为 .
三、解答题
-
19. 在△ABC中,AE平分∠BAC交BC于E,DE∥AC交AB于D,过D作DF∥BC交AC于F,若AD=3,求FC.
 20. 某校为了解全校2000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成频数分布直方图(如图所示).
20. 某校为了解全校2000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成频数分布直方图(如图所示). (1)、这50名学生在这一天课外阅读所用时间的众数是多少?(2)、这50名学生在这一天平均每人的课外阅读所用时间是多少?(3)、请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
(1)、这50名学生在这一天课外阅读所用时间的众数是多少?(2)、这50名学生在这一天平均每人的课外阅读所用时间是多少?(3)、请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?四、解答题
-
21. 先化简,再求值: ,其中x是不等式3x+7>1的负整数解.22. 如图,直线y=x﹣1与反比例函数y= 的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
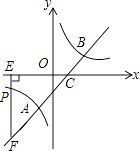 (1)、反比例函数的解析式为 , 直线y=x﹣1在双曲线y= 上方时x的取值范围是;(2)、若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.23. 某市修通一条与省会城市相连接的高速铁路,动车走高速铁路线到省会城市路程是500千米,普通列车走原铁路线路程是560千米.已知普通列车与动车的速度比是2:5,从该市到省会城市所用时间动车比普通列车少用4.5小时,求普通列车、动车的速度.24. 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
(1)、反比例函数的解析式为 , 直线y=x﹣1在双曲线y= 上方时x的取值范围是;(2)、若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.23. 某市修通一条与省会城市相连接的高速铁路,动车走高速铁路线到省会城市路程是500千米,普通列车走原铁路线路程是560千米.已知普通列车与动车的速度比是2:5,从该市到省会城市所用时间动车比普通列车少用4.5小时,求普通列车、动车的速度.24. 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
五、解答题
-
25. 如图,已知直线y=﹣x﹣(k+1)与双曲线y= 相交于B、C两点,与x轴相交于A点,BM⊥x轴交x轴于点M,S△OMB=
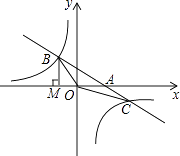 (1)、求这两个函数的解析式;(2)、若已知点C的横坐标为3,求A、C两点坐标;(3)、在(2)条件下,是否存在点P,使以A、O、C、P为顶点的四边形是平行四边形?若存在,请直接写出P点的坐标;若不存在,请说明理由.26. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)、求这两个函数的解析式;(2)、若已知点C的横坐标为3,求A、C两点坐标;(3)、在(2)条件下,是否存在点P,使以A、O、C、P为顶点的四边形是平行四边形?若存在,请直接写出P点的坐标;若不存在,请说明理由.26. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O. (1)、如图1,连接AF、CE.求证:四边形AFCE为菱形;(2)、如图1,求AF的长;(3)、如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒1cm,设运动时间为t秒.
(1)、如图1,连接AF、CE.求证:四边形AFCE为菱形;(2)、如图1,求AF的长;(3)、如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,已知点P的速度为每秒1cm,设运动时间为t秒.①问在运动的过程中,以A、C、P、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度,若不可能,请说明理由;
②若点Q的速度为每秒0.8cm,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.