2015-2016学年重庆市丰都县八年级上学期期末数学试卷
试卷更新日期:2016-11-10 类型:期末考试
一、选择题
-
1. 若分式 有意义,则x满足的条件是( )A、x≠0 B、x≠3 C、x≠﹣3 D、x≠±32. 计算:(﹣x)3•(﹣2x)的结果是( )A、﹣2x4 B、﹣2x3 C、2x4 D、2x33. 在平面直角坐标系中,点A(7,﹣2)关于x轴对称的点A′的坐标是( )A、(7,2) B、(7,﹣2) C、(﹣7,2) D、(﹣7,﹣2)4. 若△ABC≌△A′B′C′,且AB=AC=9,△ABC的周长为26cm,则B′C′的长为( )A、10cm B、9cm C、4cm D、8cm5. 如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
 A、90°﹣ α B、90°+ α C、 D、360°﹣α6. 分式方程 的解为( )A、x=﹣2 B、x=2 C、x=﹣3 D、x=37. 计算:( )2014×(﹣1.5)2015 的结果是( )A、﹣ B、 C、﹣ D、8. 下列各图形都是轴对称图形,其中对称轴最多的是( )A、等腰直角三角形 B、直线 C、等边三角形 D、正方形9. 已知△ABC的两边长分别为AB=9、AC=2,第三边BC的长为奇数,则( )A、BC=5 B、BC=7 C、BC=9 D、BC=1110. 一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )A、5 B、5或6 C、5或7 D、5或6或711. 为保证达万高速公路在2012年底全线顺利通车,某路段规定在若干天内完成修建任务.已知甲队单独完成这项工程比规定时间多用10天,乙队单独完成这项工程比规定时间多用40天,如果甲、乙两队合作,可比规定时间提前14天完成任务.若设规定的时间为x天,由题意列出的方程是( )A、 B、 C、 D、12. 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF= S△ABC , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( )
A、90°﹣ α B、90°+ α C、 D、360°﹣α6. 分式方程 的解为( )A、x=﹣2 B、x=2 C、x=﹣3 D、x=37. 计算:( )2014×(﹣1.5)2015 的结果是( )A、﹣ B、 C、﹣ D、8. 下列各图形都是轴对称图形,其中对称轴最多的是( )A、等腰直角三角形 B、直线 C、等边三角形 D、正方形9. 已知△ABC的两边长分别为AB=9、AC=2,第三边BC的长为奇数,则( )A、BC=5 B、BC=7 C、BC=9 D、BC=1110. 一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )A、5 B、5或6 C、5或7 D、5或6或711. 为保证达万高速公路在2012年底全线顺利通车,某路段规定在若干天内完成修建任务.已知甲队单独完成这项工程比规定时间多用10天,乙队单独完成这项工程比规定时间多用40天,如果甲、乙两队合作,可比规定时间提前14天完成任务.若设规定的时间为x天,由题意列出的方程是( )A、 B、 C、 D、12. 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF= S△ABC , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 分解因式:4x2﹣1= .14. 若分式 =0,则x= .15. 如图,在△ABC中,点D是BC上一点,∠BAD=84°,AB=AD=DC,则∠CAD=
 16. 如图,在△ABC中,EF是AB边的垂直平分线,AC=18cm,BC=16cm,则△BCE的周长为 cm.
16. 如图,在△ABC中,EF是AB边的垂直平分线,AC=18cm,BC=16cm,则△BCE的周长为 cm. 17. 等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是 .18. 已知 ,则 的值等于 .
17. 等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是 .18. 已知 ,则 的值等于 .三、解答题
-
19. 按要求解答.(1)、计算:5a2b÷(﹣ ab)•(2ab2)2(2)、计算:20142﹣2013×2015(3)、因式分解:a2(x﹣y)+4b2(y﹣x).20. 如图,AB∥DC,AB=DC,AC与BD相交于点O.
求证:AO=CO.
 21. 如图,在直角坐标系中,△ABC各顶点的横、纵坐标都是整数,直线m上各点的横坐标都为﹣1.
21. 如图,在直角坐标系中,△ABC各顶点的横、纵坐标都是整数,直线m上各点的横坐标都为﹣1.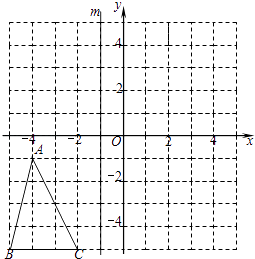 (1)、作出△ABC关于直线m的对称图形△A1B1C1;(2)、作出△ABC关于x轴对称的图形△A2B2C2;(3)、写出△A2B2C2的各顶点的坐标.22. 解分式方程: +1= .23. 先化简,再求值: ,其中x是不等式3x+7>1的负整数解.24. 如图:在等边三角形ABC中,点E在线段AB上,点D在CB的延长线上,且AE=BD,试确定线段DE与EC的大小关系,并说明理由.
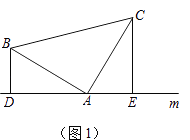
(1)、作出△ABC关于直线m的对称图形△A1B1C1;(2)、作出△ABC关于x轴对称的图形△A2B2C2;(3)、写出△A2B2C2的各顶点的坐标.22. 解分式方程: +1= .23. 先化简,再求值: ,其中x是不等式3x+7>1的负整数解.24. 如图:在等边三角形ABC中,点E在线段AB上,点D在CB的延长线上,且AE=BD,试确定线段DE与EC的大小关系,并说明理由. 25. 某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?26. 解答(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
25. 某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书数量比第一次多10本.当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?26. 解答(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
 (2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
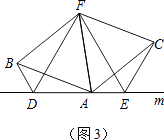
(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.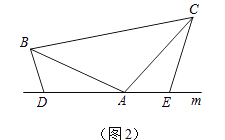 (3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.