2015-2016学年四川省绵阳市平武县八年级下学期期末数学试卷
试卷更新日期：2016-11-10 类型：期末考试
一、选择题
-
1. 下列计算正确的是（ ）A、 B、 C、 D、2. 下列函数中，y是x的正比例函数的是（ ）A、y= B、y= C、y=﹣2x+1 D、y=2x23. 如图，在直角三角形ABC中，∠C=90°，∠A=30°，BC=2 ，则AC=（ ）
A、6 B、6 C、4 D、44. 已知函数y= 中，当x=a时的函数值为1，则a的值是（ ）A、﹣1 B、1 C、﹣3 D、35. 如图，E、F、G、H分别是四边形ABCD四条边的中点，则四边形EFGH一定是（ ）
A、平行四边形 B、矩形 C、菱形 D、正方形6. 如图，在菱形ABCD中，对角线AC、BD交于点O，E为AD的中点，菱形ABCD的周长为32，则OE的长等于（ ）
A、2 B、4 C、8 D、167. 一次函数y=4x﹣2的图象可以由正比例函数y=4x的图象（ ）得到．A、向上平移2个单位 B、向下平移4个单位 C、向下平移2个单位 D、向上平移4个单位8. 下列命题是假命题的是（ ）A、平行四边形的对角相等 B、四条边都相等的四边形是菱形 C、正方形的两条对角线互相垂直 D、矩形的两条对角线互相垂直9. 某班抽取6名同学参加体能测试，成绩如下：80，90，75，75，80，80．下列表述错误的是（ ）A、众数是80 B、中位数是75 C、平均数是80 D、极差是1510. 在平面直角坐标系中，平行四边形ABCD的顶点A，B，D的坐标分别是（0，0），（5，0），（2，3），则顶点C的坐标是（ ）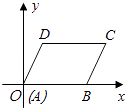
A、（3，7） B、（5，3） C、（7，3） D、（8，2）11. 若一次函数y=（m﹣3）x+（m+1）（其中m为常数）的图形经过第一、二、四象限，则m的取值范围是（ ）A、﹣1≤m≤3 B、m＜3 C、﹣1＜m＜3 D、m＞312. 如图，圆柱的底面半径是40，高为30π，一只蚂蚁在圆柱的侧面爬行，请问蚂蚁从点A爬到点B的最短路程是（ ）
A、50π B、50 C、500π D、500二、填空题
-
13. 函数y= 的自变量x的取值范围是 ．14. 一组数据7，x，8，y，10，z，6的平均数为4，则x，y，z的平均数是 ．15. 一个三角形的三边长分别为6，8，10，则这个三角形最长边上的高是 ．16. 若 ，那么x+y= ．17. 如图，一次函数y=ax+b的图象经过A（2，0）、B（0，﹣1）两点，则关于x的不等式ax+b＜0的解集是 ．
18. 如图，矩形纸片ABCD，AB=2，点E在BC上，且AE=EC，若将纸片沿AE折叠，点B恰好落在AC上，则AC的长是 ．
三、解答题
-
19. 计算：20. 如图，甲、乙两船从港口A同时出发，甲船以每小时30海里的速度向北偏东35°方向航行，乙船以每小时40海里的速度向另一方向航行，1小时后，甲船到达C岛，乙船达到B岛，若C、B两岛相距50海里，请你求出乙船的航行方向．
21. 如图，一次函数y=ax+b的图象经过点（1，2），点（﹣1，6），且与x轴交于点B，与y轴交于点A．
(1)、求出这个一次函数的解析式；(2)、求出一次函数图象与两坐标轴围成的图形的面积．22. 如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连结CE，若∠E=50°，求∠BAO的大小．
23. 为了比较市场上甲、乙两种电子钟每日走时误差的情况，从这两种电子钟中，各随机抽取10台进行测试，两种电子钟走时误差的数据如表（单位：秒）：此题图片显示不全
一
二
三
四
五
六
七
八
九
十
甲种电子钟
1
﹣3
﹣4
4
2
﹣2
2
﹣1
﹣1
2
乙种电子钟
4
﹣3
﹣1
2
﹣2
1
﹣2
2
﹣2
1
(1)、计算甲、乙两种电子钟走时误差的平均数；(2)、计算甲、乙两种电子钟走时误差的方差；(3)、根据经验，走时稳定性较好的电子钟质量更优．若两种类型的电子钟价格相同，请问：你买哪种电子钟？为什么？
