2015-2016学年山东省临沂市郯城县八年级上学期期末数学试卷
试卷更新日期:2016-11-10 类型:期末考试
一、选择题
-
1. 要使分式 有意义,则x的取值应满足( )A、x≠2 B、x≠﹣1 C、x=2 D、x=﹣12. 若三角形的三边长分别为3,4,x﹣1,则x的取值范围是( )A、0<x<8 B、2<x<8 C、0<x<6 D、2<x<63. 分式 可变形为( )A、 B、﹣ C、 D、﹣4. 下列代数运算正确的是( )A、(x3)2=x5 B、(2x)2=2x2 C、(x+1)2=x2+1 D、x3•x2=x55. 如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为( )
 A、70° B、80° C、90° D、100°6. 把多项式(m+1)(m﹣1)+(m﹣1)提取公因式(m﹣1)后,余下的部分是( )A、m+1 B、2m C、2 D、m+27. 化简 结果正确的是( )A、ab B、﹣ab C、a2﹣b2 D、b2﹣a28. 如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )
A、70° B、80° C、90° D、100°6. 把多项式(m+1)(m﹣1)+(m﹣1)提取公因式(m﹣1)后,余下的部分是( )A、m+1 B、2m C、2 D、m+27. 化简 结果正确的是( )A、ab B、﹣ab C、a2﹣b2 D、b2﹣a28. 如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正方形(a>2),将剩余部分剪开密铺成一个平行四边形,则该平行四边形的面积为( )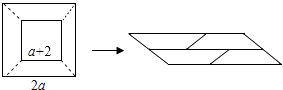 A、a2+4 B、2a2+4a C、3a2﹣4a﹣4 D、4a2﹣a﹣29. 如图,给出下列四组条件:
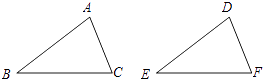
A、a2+4 B、2a2+4a C、3a2﹣4a﹣4 D、4a2﹣a﹣29. 如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E.BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
 A、1组 B、2组 C、3组 D、4组10. 已知a+b=2,则a2﹣b2+4b的值是( )A、2 B、3 C、4 D、611.
A、1组 B、2组 C、3组 D、4组10. 已知a+b=2,则a2﹣b2+4b的值是( )A、2 B、3 C、4 D、611.如图,在平面直角坐标系中,点P(﹣1,2)关于直线x=1的对称点的坐标为( )
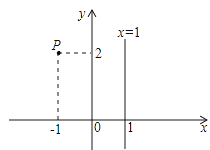 A、(1,2) B、(2,2) C、(3,2) D、(4,2)12. 已知点P(1﹣2a,a﹣2)关于y轴的对称点在第四象限内,且a为整数,则关于x的分式方程 + =2的解是( )A、3 B、1 C、5 D、不能确定13. 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A、(1,2) B、(2,2) C、(3,2) D、(4,2)12. 已知点P(1﹣2a,a﹣2)关于y轴的对称点在第四象限内,且a为整数,则关于x的分式方程 + =2的解是( )A、3 B、1 C、5 D、不能确定13. 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )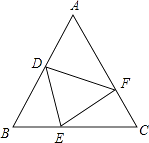 A、75° B、70° C、65° D、60°14. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则这四个结论中正确的有( )
A、75° B、70° C、65° D、60°14. 如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则这四个结论中正确的有( )①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
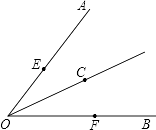
15. 计算:(2a2)3•a4= .16. 化简: = .17. 若m=2n+1,则m2﹣4mn+4n2的值是 .18. 小成每周末要到距离家5千米的体育馆打球,他骑自行车前往体育馆比乘汽车多用10分钟,乘汽车的速度是骑自行车速度的2倍.设骑自行车的速度为x千米/时,根据题意列方程为 .19. 如图,已知点C是∠AOB平分线上一点,点E,F分别在边OA,OB上,如果要得到OE=OF,需要添加以下条件中的某一个即可,请你写出所有可能结果的序号为①∠OCE=∠OCF;②∠OEC=∠OFC;③EC=FC;④EF⊥OC.
三、解答题
-
20. 分解因式:(1)、x3y﹣4x2y+4xy;(2)、a3+2a2﹣3a.21. 计算:(1)、(x﹣y)2﹣(y+2x)(y﹣2x);(2)、( ﹣ )÷ .22. 如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使CD=CA,连接AD,求∠BAD的度数.
 23. 小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?
23. 小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?

 (1)、请你帮他们解答,并说明理由.(2)、细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)(3)、小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并写出结论,不要求说明理由.(如图3)24. 从甲市到乙市乘坐高速列车的路程为180千米,乘坐普通列车的路程为240千米.高速列车的平均速度是普通列车的平均速度的3倍.高速列车的乘车时间比普通列车的乘车时间缩短了2小时.高速列车的平均速度是每小时多少千米?25. 在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形上)
(1)、请你帮他们解答,并说明理由.(2)、细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)(3)、小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并写出结论,不要求说明理由.(如图3)24. 从甲市到乙市乘坐高速列车的路程为180千米,乘坐普通列车的路程为240千米.高速列车的平均速度是普通列车的平均速度的3倍.高速列车的乘车时间比普通列车的乘车时间缩短了2小时.高速列车的平均速度是每小时多少千米?25. 在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形上) (1)、画出△ABC关于直线l:x=﹣1的对称三角形△A1B1C1;并写出A1、B1、C1的坐标.(2)、在直线x=﹣l上找一点D,使BD+CD最小,满足条件的D点为 .
(1)、画出△ABC关于直线l:x=﹣1的对称三角形△A1B1C1;并写出A1、B1、C1的坐标.(2)、在直线x=﹣l上找一点D,使BD+CD最小,满足条件的D点为 .提示:直线x=﹣l是过点(﹣1,0)且垂直于x轴的直线.
26. 如图:已知在△ABC中,∠ACB=90°,AC=BC=1,点D是AB上任意一点,AE⊥AB,且AE=BD,DE与AC相交于点F. (1)、试判断△CDE的形状,并说明理由.(2)、是否存在点D,使AE=AF?如果存在,求出此时AD的长,如果不存在,请说明理由.
(1)、试判断△CDE的形状,并说明理由.(2)、是否存在点D,使AE=AF?如果存在,求出此时AD的长,如果不存在,请说明理由.