2015-2016学年山东省临沂市平邑县八年级上学期期末数学试卷

试卷更新日期：2016-11-10 类型：期末考试

进入出卷网下载

一、选择题

1. 要使分式 $\frac{1}{x}$ 有意义，x的取值范围满足（　　）

A、x=0 B、x≠0 C、x＞0 D、x＜0

查看试题解析
2. 下列各式中能用平方差公式是（）

A、（x+y）（y+x） B、（x+y）（y﹣x） C、（x+y）（﹣y﹣x） D、（﹣x+y）（y﹣x）

查看试题解析
3. 下列计算结果正确的是（）

A、x•x²=x² B、（x⁵）³=x⁸ C、（ab）³=a³b³ D、a⁶÷a²=a³

查看试题解析
4. 下列长度的三条线段，哪一组不能构成三角形（）

A、3，3，3 B、3，4，5 C、5，6，10 D、4，5，9

查看试题解析
5. 如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（）

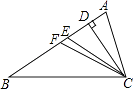A、AB=2BF B、∠ACE= $\frac{1}{2}$ ∠ACB C、AE=BE D、CD⊥BE

查看试题解析
6.
如图，将两根等长钢条AA′、BB′的中点O连在一起，使AA′、BB′可以绕着点O自由转动，就做成了一个测量工件，则AB的长等于容器内径A′B′，那么判定△OAB≌△OA′B′的理由是（　　）

A、边边边 B、边角边 C、角边角 D、角角边

查看试题解析
7. 下列计算正确的是（）

A、3²=6 B、3^﹣¹=﹣3 C、3⁰=0 D、3^﹣¹= $\frac{1}{3}$

查看试题解析
8. 已知y²+10y+m是完全平方式，则m的值是（　　）

A、25 B、±25 C、5 D、±5

查看试题解析
9. 如图，△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，则∠BDC的度数为（）

A、72° B、36° C、60° D、82°

查看试题解析
10. 在△ABC中，AD是∠BAC的平分线，且AB=AC+CD，若∠BAC=75°，则∠ABC的大小为（）

A、25° B、35° C、37.5° D、45°

查看试题解析
11. 若分式 $\frac{1}{x} - \frac{1}{y} = 2$ ，则分式 $\frac{4 x + 5 x y - 4 y}{x - 3 x y - y}$ 的值等于（）

A、﹣ $\frac{3}{5}$ B、 $\frac{3}{5}$ C、﹣ $\frac{4}{5}$ D、 $\frac{4}{5}$

查看试题解析
12. 若x²+cx+6=（x+a）（x+b），其中a，b，c为整数，则c的取值有（　　）

A、1个 B、2个 C、4个 D、8个

查看试题解析

二、填空题

13. 计算3a²b³•（﹣2ab）²= ．

查看试题解析
14. 分解因式：a²b﹣b³= ．

查看试题解析
15. 如图，∠AOP=∠BOP=15°，PC∥OA，PQ⊥OA，若PC=4，则PQ=

查看试题解析
16. 如图，将一张长方形纸片折叠成如图所示的形态，∠CBD=40°，则∠ABC= ．

查看试题解析
17. 如图，点E为等边△ABC中AC边的中点，AD⊥BC，且AD=5，P为AD上的动点，则PE+PC的最小值为．

查看试题解析
18. 若关于x的分式方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 1$ 无解，则m的值是．

查看试题解析
19. 如图，在等边△ABC中，AC=3，点O在AC上，且AO=1．点P是AB上一点，连接OP，以线段OP为一边作正△OPD，且O、P、D三点依次呈逆时针方向，当点D恰好落在边BC上时，则AP的长是．

查看试题解析

三、解答题

20. 解答下列各题：

(1)、分解因式：4a²﹣8ab+4b²﹣16c²

(2)、计算：（2a+b）（2a﹣b）+b（2a+b）﹣8a²b÷2b

(3)、化简求值：（ $\frac{3 x + 4}{x^{2} - 1}$ ﹣ $\frac{2}{x - 1}$ ）÷ $\frac{x + 2}{x^{2} - 2 x + 1}$ ，其中x=﹣3

(4)、解分式方程： $\frac{x}{x - 2}$ ﹣1= $\frac{8}{x^{2} - 4}$ ．

查看试题解析
21. 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE，BE，BE⊥AE，延长AE交BC的延长线于点F．求证：

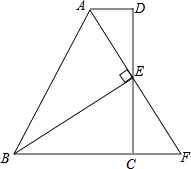(1)、FC=AD；

(2)、AB=BC+AD．

查看试题解析
22. 如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M，求证：M是BE的中点．

查看试题解析
23. 从2014年春季开始，我县农村实行垃圾分类集中处理，对农村环境进行综合整治，靓化了我们的家园．现在某村要清理一个卫生死角内的垃圾，若用甲、乙两车运送，两车各运15趟可完成，已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的3倍，求甲、乙两车单独运完此堆垃圾各需运多少趟？

查看试题解析
24. 常用的分解因式的方法有提取公因式法、公式法及到了高中还要学习的十字相乘法，但有更多的多项式只用上述方法就无法分解，x²﹣4y²﹣2x+4y，我们细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式了．过程为：x²﹣4y²﹣2x+4y=（x+2y）（x﹣2y）﹣2（x﹣2y）=（x﹣2y）（x+2y﹣2）这种分解因式的方法叫分组分解法．利用这种方法解决下列问题：

(1)、分解因式：a²﹣4a﹣b²+4；

(2)、△ABC三边a，b，c满足a²﹣ab﹣ac+bc=0，判断△ABC的形状．

查看试题解析