2015-2016学年青海省油田二中八年级下学期期末数学试卷
试卷更新日期:2016-11-10 类型:期末考试
一、填空题
-
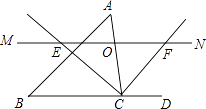
1. 计算: 的结果是 .2. 数据﹣2,﹣1,0,3,5的方差是 .3. 函数y= 中自变量x的取值范围是 .4. 一次函数y=﹣3x+6的图象不经过象限.5. 某一次函数的图象经过点(﹣1,3),且函数y随x的增大而减小,请你写出一个符合条件的函数解析式 .6. 在△ABC中,∠C=90°,若a+b=7cm,c=5cm,则△ABC的面积为 .7. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为 .
 8. 如图,函数y=ax﹣1的图象过点(1,2),则不等式ax﹣1>2的解集是 .
8. 如图,函数y=ax﹣1的图象过点(1,2),则不等式ax﹣1>2的解集是 . 9. 在一次函数y=(2﹣k)x+1中,y随x的增大而增大,则k的取值范围为 .10. 平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=cm.11. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
9. 在一次函数y=(2﹣k)x+1中,y随x的增大而增大,则k的取值范围为 .10. 平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=cm.11. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .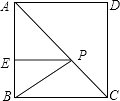 12. 某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取 .
12. 某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取 .候选人
甲
乙
丙
丁
测试成绩(百分制)
面试
86
92
90
83
笔试
90
83
83
92
13. 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD的周长为 . 14. 在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .15. 如图,在▱ABCD中,对角线AC与BD相交于点O,请添加一个条件 , 使▱ABCD成为菱形(写出符合题意的一个条件即可)
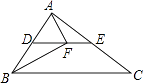
14. 在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .15. 如图,在▱ABCD中,对角线AC与BD相交于点O,请添加一个条件 , 使▱ABCD成为菱形(写出符合题意的一个条件即可) 16. 如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 .
16. 如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 .
二、选择题
-
17. 二次根式、、、、、中,最简二次根式有( )个.A、1个 B、2个 C、3个 D、4个18. 下列各组数中,以a,b,c为边的三角形不是直角三角形的是( )A、a=1.5,b=2,c=3 B、a=7,b=24,c=25 C、a=6,b=8,c=10 D、a=3,b=4,c=519. 期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”,上面两位同学的话能反映出的统计量是( )A、众数和平均数 B、平均数和中位数 C、众数和方差 D、众数和中位数20. 已知一次函数y=2x+a,y=﹣x+b的图象都经过A(﹣2,0),且与y轴分别交于B、C两点,则△ABC的面积为( )A、4 B、5 C、6 D、721. 如图,在▱ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
 A、4 B、3 C、 D、222. 如图所示,函数y1=|x|和 的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是( )
A、4 B、3 C、 D、222. 如图所示,函数y1=|x|和 的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是( ) A、x<﹣1 B、﹣1<x<2 C、x>2 D、x<﹣1或x>223. 如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A、x<﹣1 B、﹣1<x<2 C、x>2 D、x<﹣1或x>223. 如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( ) A、
A、 B、
B、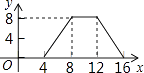 C、
C、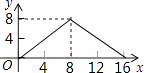 D、
D、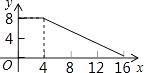 24. 为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表,关于这10户家庭的月用电量说法正确的是( )
24. 为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表,关于这10户家庭的月用电量说法正确的是( )月用电量(度)
25
30
40
50
60
户数
1
2
4
2
1
A、极差是3 B、众数是4 C、中位数40 D、平均数是20.525. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )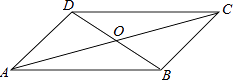 A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC26.
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC26.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
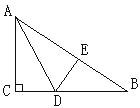 A、2cm B、3cm C、4cm D、5cm
A、2cm B、3cm C、4cm D、5cm三、解答题
-
27. 当x=2﹣ 时,求代数式(7+4 )x2+(2+ )x+ 的值.28. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
 (1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.29. 如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.29. 如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点. (1)、求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;(2)、当△OPA的面积为10时,求点P的坐标.30. 我市某医药公司要把药品运往外地,现有两种运输方式可供选择,
(1)、求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;(2)、当△OPA的面积为10时,求点P的坐标.30. 我市某医药公司要把药品运往外地,现有两种运输方式可供选择,方式一:使用快递公司的邮车运输,装卸收费400元,另外每公里再加收4元;
方式二:使用铁路运输公司的火车运输,装卸收费820元,另外每公里再加收2元,
(1)、请分别写出邮车、火车运输的总费用y1(元)、y2(元)与运输路程x(公里)之间的函数关系式;(2)、你认为选用哪种运输方式较好,为什么?31. 某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.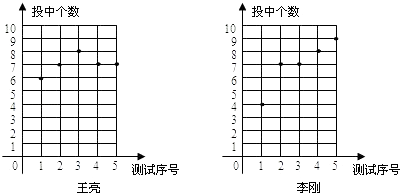 (1)、请你根据图中的数据,填写下表;
(1)、请你根据图中的数据,填写下表;姓名
平均数
众数
方差
王亮
7
李刚
7
2.8
(2)、你认为谁的成绩比较稳定,为什么?(3)、若你是教练,你打算选谁?简要说明理由.