2015-2016学年河南省信阳市固始县八年级下学期期末数学试卷

试卷更新日期：2016-11-09 类型：期末考试

进入出卷网下载

一、选择题

1. 如果 $\sqrt{{(2 a - 1)}^{2}}$ =1﹣2a，则（）

A、a＜ $\frac{1}{2}$ B、a≤ $\frac{1}{2}$ C、a＞ $\frac{1}{2}$ D、a≥ $\frac{1}{2}$

查看试题解析
2. 数据2，3，5，5，4的众数是（）

A、2 B、3 C、4 D、5

查看试题解析
3. 如图，在菱形ABCD中，AB=5，∠BCD=120°，则对角线AC等于（）

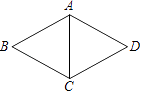A、20 B、15 C、10 D、5

查看试题解析
4. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（）

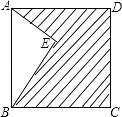A、48 B、60 C、76 D、80

查看试题解析
5. 实数a，b在数轴上的位置如图所示，则化简 $\sqrt{a^{2}} - \sqrt{b^{2}} - \sqrt{{(a - b)}^{2}}$ 的结果是（）

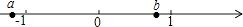A、﹣2b B、﹣2a C、2（b﹣a） D、0

查看试题解析
6. 如图，一圆柱高8cm，底面半径为 $\frac{6}{π}$ cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是（）

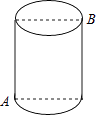A、6cm B、8cm C、10cm D、12cm

查看试题解析
7. “龟兔首次赛跑“之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的图象刻画了“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的时间，y₁表示乌龟所行的路程，y₂表示兔子所行的路程）．有下列说法：
①“龟兔再次赛跑”的路程为1000米
②兔子和乌龟同时从起点出发
③乌龟在途中休息了10分钟
④兔子在途中750米处追上乌龟
其中说法正确的是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在正方形ABCD中，AB=1，连接AC，以AC为边作第一个正方形ACC₁D₁ ，连接AC₁ ，以AC₁为边作第二个正方形AC₁C₂D₂ ，则第10个正方形边长为（）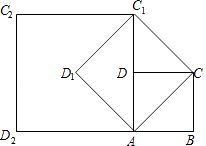

A、8 B、16 C、32 D、64

查看试题解析

二、填空题

9. 已知函数y=（m+2）x+m²﹣4是一次函数，则m ．

查看试题解析
10. 顺次连接矩形各边中点所得四边形为形．

查看试题解析
11. 已知 $\sqrt{12 - n}$ 是正整数，则实数n的最大值为．

查看试题解析
12. 三角形的两边长分别为3和5，要使这个三角形是直角三角形，则第三边长是．

查看试题解析
13. 如图，正方形ABCD中，M在DC上，且BM=10，N是AC上一动点，则DN+MN的最小值为．

查看试题解析
14. 在平面直角坐标系中，点A，B的坐标分别为（m，3），（3m﹣1，3），若线段AB与直线y=2x+1相交，则m的取值范围为．

查看试题解析
15. 如图，在矩形纸片ABCD中，AB=3，BC=5，点E、F是BC、CD边上的动点（包括端点处），若将纸片沿EF折叠，使得点C恰好落在AD边上点P处．设CF=x，则x的取值范围为．

查看试题解析

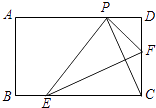
三、解答题

16. 计算：3 $\sqrt{3}$ ﹣ $\sqrt{8}$ + $\sqrt{2}$ ﹣ $\sqrt{27}$ ．

查看试题解析
17. 计算：（2 $\sqrt{5}$ +5 $\sqrt{2}$ ）（5 $\sqrt{2}$ ﹣2 $\sqrt{5}$ ）﹣（ $\sqrt{5}$ ﹣ $\sqrt{2}$ ）² ．

查看试题解析
18. 如图，在▱ABCD中，E，F分别为边AB，CD的中点，连接DE、BF、BD．

(1)、求证：△ADE≌△CBF．

(2)、若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．

查看试题解析
19. 小明同学骑自行车去新华书店，如图表示他离家的距离y（千米）与所用的时间s（小时）之间关系的函数图象

(1)、根据图象回答：小明家离新华书店千米，小明用了小时到达新华书店；

(2)、小明从家出发两个半小时走了千米；

(3)、直线CD的函数解析式为；

(4)、小明出发小时，离家12千米．

查看试题解析
20. 观察下面的变形规律：
$\frac{1}{\sqrt{2} + 1}$ = $\sqrt{2} - 1$ ， $\frac{1}{\sqrt{3} + \sqrt{2}}$ = $\sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}}$ = $\sqrt{4} - \sqrt{3}$ ， $\frac{1}{\sqrt{5} + \sqrt{4}}$ = $\sqrt{5} - \sqrt{4}$ ，…
解答下面的问题：

(1)、若n为正整数，请你猜想 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ =；

(2)、计算：（ $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}}$ + $\frac{1}{\sqrt{4} + \sqrt{3}}$ +…+ $\frac{1}{\sqrt{2016} + \sqrt{2015}}$ ）×（ $\sqrt{2016} + 1$ ）

查看试题解析
21. 在△ABC中，∠C=90°，AC=6，BC=8，D、E分别是斜边AB和直角边CB上的点，把△ABC沿着直线DE折叠，顶点B的对应点是B′．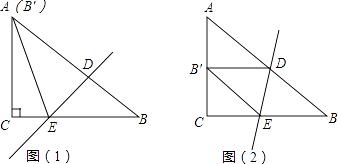

(1)、如图（1），如果点B′和顶点A重合，求CE的长；

(2)、如图（2），如果点B′和落在AC的中点上，求CE的长．

查看试题解析
22. 固始县教体局举办”我的中国梦“为主题的知识竞赛，甲、乙两所学校参赛人数相等．比赛结束后，发现学生成绩分别为70分，80分，90分，100分，并依据统计数据绘制了如下不完整的统计图表．
乙校成绩统计表
分数（分）
70分
80分
90分
100分
人数（人）
7
1
8

(1)、在图①中，“80分”所在扇形的圆心角度数为．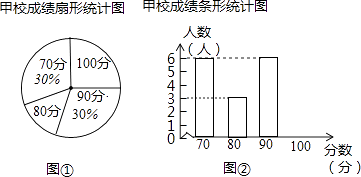

(2)、请你将图②补充完整．

(3)、通过计算，说明哪所学校的学生成绩较整齐．

查看试题解析
23. 某服装公司招工广告承诺：熟练工人每月工资至少3000元．每天工作8小时，一个月工作25天．月工资底薪800元，另加计件工资．加工1件A型服装计酬16元，加工1件B型服装计酬12元．在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时，加工3件A型服装和1件B型服装需7小时．（工人月工资=底薪+计件工资）

(1)、一名熟练工加工1件A型服装和1件B型服装各需要多少小时？

(2)、一段时间后，公司规定：“每名工人每月必须加工A，B两种型号的服装，且加工A型服装数量不少于B型服装的一半”．设一名熟练工人每月加工A型服装a件，工资总额为W元．请你运用所学知识判断该公司在执行规定后是否违背了广告承诺？

查看试题解析
24. 问题探究：

(1)、
已知：如图1，在正方形ABCD中，点E、H分别在BC、AB上，若AE⊥DH于点O，求证AE=DH；
类比探究：

(2)、如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，探究线段EF与HG的数量关系，并说明理由；
拓展应用：

(3)、已知，如图3，在（2）问条件下，若BC=4，E为BC的中点，AF= $\frac{1}{4}$ AD，求HG的长

查看试题解析

分数（分）	70分	80分	90分	100分
人数（人）	7		1	8