2015-2016学年天津市津南区东片学区九年级下学期期中数学试卷
试卷更新日期：2016-11-09 类型：期中考试
一、选择题
-
1. tan60°的值等于（ ）
A、3 B、 C、 D、2. 在下列图案中，是中心对称图形的是（ ）A、
B、
C、
D、
3.如图，这是由5个大小相同的小正方体摆成的立体图形，它的俯视图是（ ）
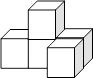A、
B、
C、
D、
4. 若m= ﹣2，则估计m的值所在的范围是（ ）A、1＜m＜2 B、2＜m＜3 C、3＜m＜4 D、4＜m＜55. 正六边形的边心距与边长之比为（ ）A、 ：3 B、 ：2 C、1：2 D、 ：26. 如图是某班40名学生一分钟跳绳测试成绩（次数为整数）的频数分布直方图，从左起第一、二、三、四个小长方形的高的比为1：4：3：2，那么该班一分钟跳绳次数在100次以上的学生有（ ）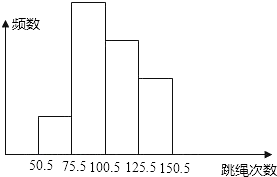
A、6人 B、8人 C、16人 D、20人7. 等腰三角形一条边的边长为3，它的另两条边的边长是关于x的一元二次方程x2﹣12x+k=0的两个根，则k的值是（ ）A、27 B、36 C、27或36 D、188. 如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（ ）
A、2 B、 C、 D、69. 如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A=22.5°，OC=4，CD的长为（ ）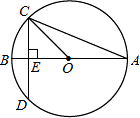
A、2 B、4 C、4 D、810.甲、乙两人沿相同的路线由A地到B地匀速前进，A、B两地间的路程为20km．他们前进的路程为s（km），甲出发后的时间为t（h），甲、乙前进的路程与时间的函数图象如图所示．根据图象信息，下列说法正确的是（ ）
A、甲的速度是4km/h B、乙的速度是10km/h C、乙比甲晚出发1h D、甲比乙晚到B地3h11. 二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x=2，下列结论：①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④当x＞﹣1时，y的值随x值的增大而增大．
其中正确的结论有（ ）
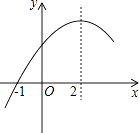A、1个 B、2个 C、3个 D、4个二、填空题
-
12. 方程 ﹣ =0的解是 ．13. 如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为 ．
14. 如图，转盘中8个扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 ．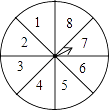
15.如图，A，B，C是⊙O上的三点，∠CAO=25°，∠BCO=35°，则∠AOB=度．
16. 如图，正方形ABCD的边长为6，E为BC上的一点，BE=2，F为AB上的一点，AF=3，P为AC上一点，则PF+PE的最小值为 ．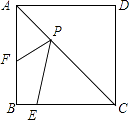
17. 如图，将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上．
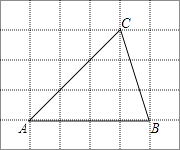(1)、△ABC的面积等于；(2)、若四边形DEFG是△ABC中所能包含的面积最大的正方形，请你在如图所示的网格中，用直尺和三角尺画出该正方形，并简要说明画图方法（不要求证明） ．三、解答题
-
18. 解不等式组 ，并把它的解集在数轴上表示出来．
19. 某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组（A：39.5～46.5；B：46.5～53.5；C：53.5～60.5；D：60.5～67.5；E：67.5～74.5），并依据统计数据绘制了如下两幅尚不完整的统计图．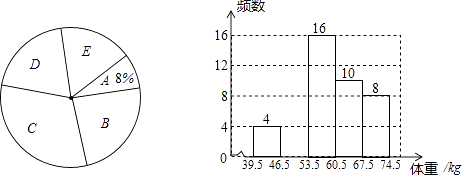
解答下列问题：
(1)、这次抽样调查的样本容量是 ， 并补全频数分布直方图；(2)、C组学生的频率为 ， 在扇形统计图中D组的圆心角是度；(3)、请你估计该校初三年级体重超过60kg的学生大约有多少名？20. 如图，在△ABC中，∠C=90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB于点F，⊙O是△BEF的外接圆．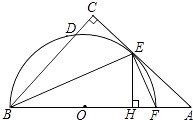
(1)、求证：AC是⊙O的切线．(2)、过点E作EH⊥AB于点H，求证：CD=HF．21.如图，为了测量某风景区内一座塔AB的高度，小明分别在塔的对面一楼房CD的楼底C，楼顶D处，测得塔顶A的仰角为45°和30°，已知楼高CD为10m，求塔的高度（结果精确到0.1m）．（参考数据： ≈1.41， ≈1.73）
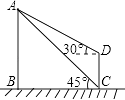22. 某超市为了回馈广大新老客户，元旦期间决定实行优惠活动．优惠一：非会员购物所有商品价格可获九折优惠；
优惠二：交纳200元会费成为该超市的一员，所有商品价格可优惠八折优惠．
(1)、若用x（元）表示商品价格，请你用含x的式子分别表示两种购物优惠后所花的钱数；(2)、当商品价格是多少元时，两种优惠后所花钱数相同；(3)、若某人计划在该超市购买价格为2700元的一台电脑，请分析选择那种优惠更省钱？23.如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．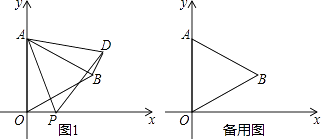
(1)、求B的坐标；(2)、当点P运动到点（t，0）时，试用含t的式子表示点D的坐标；(3)、是否存在点P，使△OPD的面积等于 ，若存在，请求出符合条件的点P的坐标（直接写出结果即可）24.如图，抛物线y=﹣x2+bx+c与直线y= x+2交于C、D两点，其中点C在y轴上，点D的坐标为（3， ）．点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F．
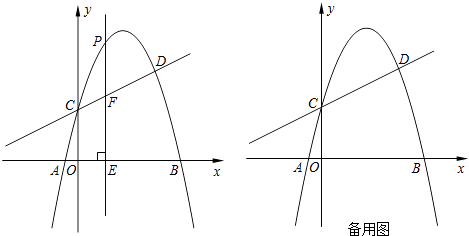(1)、求抛物线的解析式；(2)、若点P的横坐标为m，当m为何值时，以O、C、P、F为顶点的四边形是平行四边形？请说明理由．(3)、若存在点P，使∠PCF=45°，请直接写出相应的点P的坐标．