2015-2016学年江西省赣州市赣县二中九年级下学期期中数学试卷
试卷更新日期:2016-11-09 类型:期中考试
一、选择题
-
1. 一元二次方程x2﹣1=0的根是( )A、1 B、﹣1 C、 D、±12. 二次函数 的顶点坐标是( )A、(3,2) B、(3,﹣2) C、(﹣3,﹣2) D、(﹣3,2)3. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
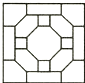 B、
B、 C、
C、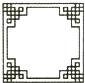 D、
D、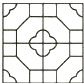 4. 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
4. 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( ) A、2.5 B、2 C、2.4 D、35. 如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
A、2.5 B、2 C、2.4 D、35. 如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )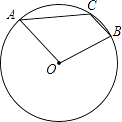 A、130° B、125° C、120° D、115°6. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
A、130° B、125° C、120° D、115°6. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:①2a﹣b=0;
②abc>0;
③4ac﹣b2<0;
④9a+3b+c<0;
⑤关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
⑥8a+c<0.
其中正确的个数是( )
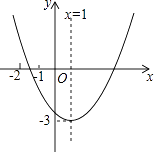 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
7. 若x=1是一元二次方程x2﹣a=0的一个根,则a= .8. 抛物线y=ax2﹣2ax+3(a≠0)的对称轴是直线x= .9. ⊙O中的弦AB长等于半径长,则弦AB所对的圆周角是 .10. 关于x的一元二次方程ax2+bx+ =0有两个相等的实数根,写一组满足条件的实数a,b的值,a= , b= .11.
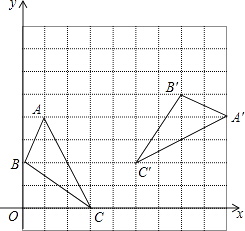
如图所示,在直角坐标系中,△A′B′C′是由△ABC绕点P旋转一定的角度而得,其中A(1,4),B(0,2),C(3,0),则旋转中心点P的坐标是 .
 12. 当x=m和x=n(m≠n)时,二次函数y=x2﹣2x+3的函数值相等,当x=m+n时,函数y=x2﹣2x+3的值为 .13. 在直角坐标系中,已知⊙O是以原点O为圆心,1为半径,若直线y=x+a与⊙O有公共点,则a的取值范围是 .14. 如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是 .
12. 当x=m和x=n(m≠n)时,二次函数y=x2﹣2x+3的函数值相等,当x=m+n时,函数y=x2﹣2x+3的值为 .13. 在直角坐标系中,已知⊙O是以原点O为圆心,1为半径,若直线y=x+a与⊙O有公共点,则a的取值范围是 .14. 如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是 .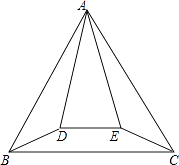
三、本大题共四小题
-
15. 解方程:4x2=(x﹣3)2(用因式分解法)16. 已知关于x的一元二次方程x2﹣kx+k﹣1=0.(1)、求证:此一元二次方程恒有实数根.(2)、无论k为何值,该方程有一根为定值,请求出此方程的定值根.17.
作图题:在⊙O 中,点D是劣弧AB的中点,仅用无刻度的直尺画线的方法,按要求完下列作图:
在图(1)中作出∠C的平分线;在图(2)中画一条弦,平分△ABC的面积.
 18. 已知抛物线l1的最高点为P(3,4),且经过点A(0,1),将抛物线l1绕原点O旋转180°后,得到抛物线l2 , 求l2的解析式.
18. 已知抛物线l1的最高点为P(3,4),且经过点A(0,1),将抛物线l1绕原点O旋转180°后,得到抛物线l2 , 求l2的解析式.四、本大题共4小题
-
19. 如图,在方格网中已知格点△ABC和点O.
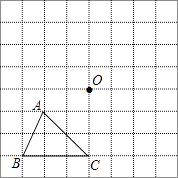 (1)、画△A′B′C′和△ABC关于点O成中心对称;(2)、请在方格网中标出所有使以点A、O、C′、D为顶点的四边形是平行四边形的D点.20.
(1)、画△A′B′C′和△ABC关于点O成中心对称;(2)、请在方格网中标出所有使以点A、O、C′、D为顶点的四边形是平行四边形的D点.20.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).
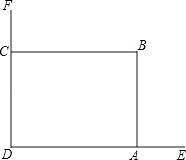 (1)、如何才能围成矩形花园的面积为75m2?(2)、能够围成面积为101m2的矩形花园吗?如能说明围法,如不能,说明理由.21. 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)、如何才能围成矩形花园的面积为75m2?(2)、能够围成面积为101m2的矩形花园吗?如能说明围法,如不能,说明理由.21. 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.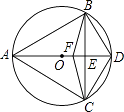 (1)、求证:BE=CE;(2)、试判断四边形BFCD的形状,并说明理由;(3)、若BC=AD=8,求CD的长.22. 某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)、求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该商品每天的销售利润最大;(3)、商场的营销部在调控价格方面,提出了A,B两种营销方案.
(1)、求证:BE=CE;(2)、试判断四边形BFCD的形状,并说明理由;(3)、若BC=AD=8,求CD的长.22. 某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)、求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该商品每天的销售利润最大;(3)、商场的营销部在调控价格方面,提出了A,B两种营销方案.方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
五、本大题共一小题
-
23. 已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m﹣5,2).(1)、问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90°?若存在,求出m的取值范围;若不存在,请说明理由.(2)、当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
六、本大题一小题
-
24. 如图,二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒 个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
 (1)、求二次函数的解析式;(2)、如图1,当△BPQ为直角三角形时,求t的值;(3)、如图2,过点Q作QN⊥x轴于N,交抛物线于点M,连结MC,MB,当t为何值时,△MCB的面积最大,并求出此时点M的坐标和△MCB面积的最大值.
(1)、求二次函数的解析式;(2)、如图1,当△BPQ为直角三角形时,求t的值;(3)、如图2,过点Q作QN⊥x轴于N,交抛物线于点M,连结MC,MB,当t为何值时,△MCB的面积最大,并求出此时点M的坐标和△MCB面积的最大值.
-