2015-2016学年江西省抚州市崇仁县九年级下学期期中数学试卷
试卷更新日期：2016-11-09 类型：期中考试
一、选择题
-
1. 在3、﹣5、0、2这四个数中，最小的一个数是（ ）A、3 B、﹣5 C、0 D、22. 函数 中，自变量x的取值范围是（ ）A、x≥2 B、x＞2 C、x＜2 D、x≠23. 今年3月21日到武汉大学赏樱花的人数约为213000人，数213000用科学记数法表示为（ ）A、21.3×104 B、213×103 C、2.13×105 D、2.13×1044. 下列计算正确的是（ ）A、b2•b2=2b2 B、（x﹣3）2=x2﹣9 C、（a5）2=a7 D、（﹣2a）2=4a25.
如图，在平面直角坐标系中，有两条位置确定的抛物线，它们的对称轴相同，则下列关系不正确的是（ ）
A、k=n B、h=m C、k＜n D、h＜0，k＜0二、填空题
-
6. 计算：﹣17+8=7. 分解因式：4a﹣ab2= ．8. 求值：sin60°﹣tan30°=
9. 小明制作了九张卡片，上面分别标有1，2，…，9这九个数字，从中随机抽取一张，所标数字恰好能被2整除的概率是 ．10. 当x=时， 分式没有意义．11.已知O为△ABC的内心，且∠BOC=130°，则∠A= ．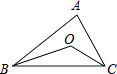
12. 如果△ABC与△DEF相似，△ABC的三边之比为3：4：6，△DEF的最长边是10cm，那么△DEF的最短边是 cm．13.如图，矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上，点G为矩形对角线的交点，经过点G的双曲线y= 在第一象限的图象与BC相交于点M，交AB于N，若已知S△MBN=9，则k的值为 ．
三、解答题
-
14. 先化简，再求值：（ x2y+xy+ y）÷（xy+y），其中x=1，y=2．15. 已知直线y=kx﹣7经过点（2，﹣1），求关于x的不等式kx﹣7≥0的解集．
16. 如图，点E、F分别是▱ABCD的边BC、AD上的点，且CE=AF．求证：△ABE≌△CDF．
17. 海南有丰富的旅游产品．某校九年级（1）班的同学就部分旅游产品的喜爱情况对游客随机调查，要求游客在列举的旅游产品中选出喜爱的产品，且只能选一项．以下是同学们整理的不完整的统计图：
根据以上信息完成下列问题：
(1)、请将条形统计图补充完整；(2)、随机调查的游客有人；在扇形统计图中，A部分所占的圆心角是度；(3)、请根据调查结果估计在1500名游客中喜爱攀锦的约有人．四、解答题
-
18. 某市百货大楼服装柜在销售中发现：“七彩”牌童装平均每天可售出20件，每件盈利40元．为了迎接元旦，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽量减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？19. 如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．
(1)、求证：直线CD为⊙O的切线；(2)、当AB=2BE，且CE= 时，求AD的长．20. 如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（﹣2，4）、（﹣2，0）、（﹣4，1），将△ABC绕原点O旋转180度得到△A1B1C1 ． 结合所给的平面直角坐标系解答下列问题：
(1)、画出△A1B1C1；(2)、画出一个△A2B2C2 ， 使它分别与△ABC，△A1B1C1轴对轴（其中点A，B，C与点A2 ， B2 ， C2对应）；(3)、在（2）的条件下，若过点B的直线平分四边形ACC2A2的面积，请直接写出该直线的函数解析式．五、解答题
-
21.
在一次暑假旅游中，小亮在仙岛湖的游船上（A处），测得湖西岸的山峰太婆尖（C处）和湖东岸的山峰老君岭（D处）的仰角都是45°．游船向东航行100米后（B处），测得太婆尖，老君岭的仰角分别为30°，60°．试问太婆尖、老君岭的高度为多少米？
22.如图，Rt△ABC中，∠BAC=90°，AB=2，AC=4，D是BC边上一动点，G是BC边上的一动点，GE∥AD分别交AC、BA或其延长线于F、E两点
(1)、如图1，当BC=5BD时，求证：EG⊥BC；(2)、如图2，当BD=CD时，FG+EG是否发生变化？证明你的结论；(3)、当BD=CD，FG=2EF时，DG的值= ．六、解答题
-
23. 如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．
(1)、求这条抛物线的解析式；(2)、E为抛物线上一动点，是否存在点E，使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；(3)、若将直线BC平移，使其经过点A，且与抛物线相交于点D，连接BD，试求出∠BDA的度数．