2015-2016学年湖北省宜昌十六中九年级上学期期中数学试卷

试卷更新日期：2016-11-09 类型：期中考试

进入出卷网下载

一、选择题

1.
通过平移，可将如图移动到下列（）

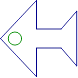A、 B、 C、 D、

查看试题解析
2. 点P（1，2）关于原点的对称点P′的坐标为（）

A、（2，1） B、（﹣1，﹣2） C、（1，﹣2） D、（﹣2，﹣1）

查看试题解析
3. 用配方法解方程x²﹣2x﹣1=0，经过配方，得到（）

A、（x+1）²=3 B、（x﹣1）²=2 C、（x﹣1）²=3 D、（x﹣2）²=5

查看试题解析
4. 方程x²﹣9=0的解是（　　）

A、x=3 B、x=9 C、x=±3 D、x=±9

查看试题解析
5. 对于二次函数y=（x﹣1）²+2的图象，下列说法正确的是（）

A、开口向下 B、顶点坐标是（1，2） C、对称轴是x=﹣1 D、有最大值是2

查看试题解析
6.
如图，一块等腰直角的三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置，使A、C、B′三点共线，那么旋转角度的大小为（）

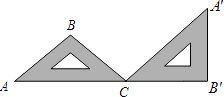A、45° B、90° C、120° D、135°

查看试题解析
7. 若二次函数y=ax²的图象经过点P（﹣3，2），则a的值为（）

A、 $\frac{2}{9}$ B、 $\frac{9}{4}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{9}$

查看试题解析
8. 已知方程x²+x﹣6=0的两个根是a，b，则ab的值为（）

A、1 B、﹣1 C、6 D、﹣6

查看试题解析
9.
如图，△ABC由△A′B′C′绕O点旋转180°而得到，则下列结论不成立的是（）

A、点A与点A′是对应点 B、BO=B′O C、∠ACB=∠C′A′B′ D、AB∥A′B′

查看试题解析
10. 下列方程中有实数根的是（）

A、x²+x+2=0 B、x²﹣x+2=0 C、x²﹣x﹣1=0 D、x²﹣x+3=0

查看试题解析
11. 有一人患了流感，经过两轮传染后共有100人患了流感，每轮传染中平均一个人传染的人数x满足的方程为（）

A、1+x+x（1+x）=100 B、x（1+x）=100 C、1+x+x²=100 D、x²=100

查看试题解析
12. 如图，二次函数y=ax²+bx+c的图象与x轴相交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（）

A、x＜﹣2 B、﹣2＜x＜4 C、x＞0 D、x＞4

查看试题解析

13. 下面表格列出了函数y=ax²+bx+c（a，b、c是常数，且a≠0），部分x与y对应值，那么方程ax²+bx+c=0的一个根x的取值范围是（　　）

x	6.17	6.18	6.19	6.20
y	﹣0.03	﹣0.01	0.02	0.04

A、 6＜x＜6.7 B、6.7＜x＜6.18 C、6.18＜x＜6.19 D、6.9＜x＜9.20

查看试题解析

14.
如图是一张长8cm、宽5cm的矩形纸板，将纸板四个角各剪去一个同样的正方形，可制成底面积是18cm²的一个无盖长方体纸盒，设剪去的正方形边长为xcm，那么x满足的方程是（）

A、40﹣4x²=18 B、（8﹣2x）（5﹣2x）=18 C、40﹣2（8x+5x）=18 D、（8﹣2x）（5﹣2x）=9

查看试题解析
15. 如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论，其中正确结论是（）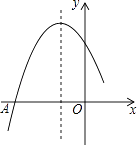

A、b²＜4ac B、2a+b=0 C、a+b+c＞0 D、若点B（ $\frac{5}{2}$ ，y₁）、C（ $\frac{1}{2}$ ，y₂）为函数图象上的两点，则y₁＜y₂

查看试题解析

二、解答题

16. 解方程：

(1)、2x²﹣7x+3=0

(2)、x（x﹣2）=x．

查看试题解析
17. 关于x的一元二次方程x²+2x+k+1=0的实数解是x₁和x₂ ．

(1)、求k的取值范围；

(2)、如果x₁+x₂﹣x₁x₂＜﹣1且k为整数，求k的值．

查看试题解析
18. △ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：

(1)、画出△ABC关于原点O的中心对称图形△A₁B₁C₁；

(2)、画出将△ABC绕点A逆时针旋转90°得到△AB₂C₂ ，

(3)、△A₁B₁C₁中顶点A₁坐标为．

查看试题解析
19. 如图，已知四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．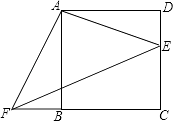

(1)、填空：△ABF可以由△ADE绕旋转中心点，按逆时针方向旋转度得到；

(2)、若BC=8，DE=6，求△AEF的面积．

查看试题解析
20.
如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径CD为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．

(1)、如图，建立直角坐标系，求此抛物线的解析式；

(2)、如果竖直摆放7个圆柱形桶时，网球能不能落入桶内？

(3)、当竖直摆放圆柱形桶至多多少个时，网球可以落入桶内？

查看试题解析
21. 已知，如图，直线l经过A（4，0）和B（0，4）两点，抛物线y=a（x﹣h）²的顶点为P（1，0），直线l与抛物线的交点为M．

(1)、求直线l的函数解析式；

(2)、若S_△_AMP=3，求抛物线的解析式．

查看试题解析
22. 宜兴科技公司生产销售一种电子产品，该产品总成本包括技术成本、制造成本、销售成本三部分，经核算，2013年该产品各部分成本所占比例约为2：a：1．且2013年该产品的技术成本、制造成本分别为400万元、1400万元．

(1)、确定a的值，并求2013年产品总成本为多少万元；

(2)、为降低总成本，该公司2014年及2015年增加了技术成本投入，确保这两年技术成本都比前一年增加一个相同的百分数m（m＜50%），制造成本在这两年里都比前一年减少一个相同的百分数2m；同时为了扩大销售量，2015年的销售成本将在2013年的基础上提高10%，经过以上变革，预计2015年该产品总成本达到2013年该产品总成本的 $\frac{4}{5}$ ，求m的值．

查看试题解析
23. 如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若点B，P在直线a的异侧，BM⊥直线a于点M．CN⊥直线a于点N，连接PM，PN．

(1)、延长MP交CN于点E（如图2）．
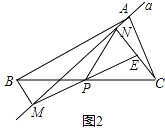
①求证：△BPM≌△CPE；
②求证：PM=PN；

(2)、若直线a绕点A旋转到图3的位置时，点B，P在直线a的同侧，其它条件不变，此时PM=PN还成立吗？若成立，请给予证明；若不成立，请说明理由；

(3)、若直线a绕点A旋转到与BC边平行的位置时，其它条件不变，请直接判断四边形MBCN的形状及此时PM=PN还成立吗？不必说明理由．

查看试题解析
24. 在平面直角坐标系xOy中，已知抛物线y=x²﹣2mx+m²﹣9．

(1)、求证：无论m为何值，该抛物线与x轴总有两个交点；

(2)、该抛物线与x轴交于A，B两点，点A在点B的左侧，且OA＜OB，与y轴的交点坐标为（0，﹣5），求此抛物线的解析式；

(3)、在（2）的条件下，抛物线的对称轴与x轴的交点为N，若点M是线段AN上的任意一点，过点M作直线MC⊥x轴，交抛物线于点C，记点C关于抛物线对称轴的对称点为D，点P是线段MC上一点，且满足MP= $\frac{1}{4}$ MC，连结CD，PD，作PE⊥PD交x轴于点E，问是否存在这样的点E，使得PE=PD？若存在，求出点E的坐标；若不存在，请说明理由．

查看试题解析