2015-2016学年湖北省宜昌二十四中九年级上学期期中数学试卷
试卷更新日期：2016-11-09 类型：期中考试
一、选择题
-
1. 将一元二次方程3x2﹣1=4x化成一般形式为（ ）A、3x2+4x=1 B、3x2﹣4x=1 C、3x2﹣4x﹣1=0 D、3x2+4x﹣1=02. 一元二次方程x2﹣3x=0的根是（ ）A、x=3 B、x1=0，x2=﹣3 C、x1=0，x2= D、x1=0，x2=33. 下列图形中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
4. 二次函数y=x2+4x﹣5的图象的对称轴为（ ）A、x=4 B、x=﹣4 C、x=2 D、x=﹣25. 抛物线y=﹣2（x﹣1）2+3的顶点坐标是（ ）A、（﹣1，3） B、（1，3） C、（1，﹣3） D、（﹣1，﹣3）6. 在平面直角坐标系内，点P（﹣2，3）关于原点的对称点Q的坐标为（ ）A、（2，﹣3） B、（2，3） C、（3，﹣2） D、（﹣2，﹣3）7. 在平面直角坐标系中，二次函数y=a（x﹣h）2（a≠0）的图象可能是（ ）A、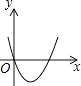
B、
C、
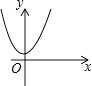D、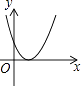
8. 学校早上8时上第一节课，45分钟后下课，这节课中分针转动的角度为（ ）A、45° B、90° C、180° D、270°9. 把抛物线y=﹣ 经（ ）平移得到y=﹣ ﹣1．A、向右平移2个单位，向上平移1个单位 B、向右平移2个单位，向下平移1个单位 C、向左平移2个单位，向上平移1个单位 D、向左平移2个单位，向下平移1个单位10. 已知关于x的方程x2+2x+m=0的有两个相等的实数根，则m为（ ）A、2 B、﹣2 C、1 D、﹣111.二次函数y=﹣x2+2x+k的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+k=0的一个解x1=3，另一个解x2=（ ）
A、1 B、﹣1 C、﹣2 D、012. 抛物线y=ax2（a＞0）的图象一定经过（ ）A、第一、二象限 B、第二、三象限 C、第二、四象限 D、第三、四象限13. 如图所示，在等腰直角△ABC中，∠B=90°，将△ABC绕点 A逆时针旋转60°后得到的△AB′C′，则∠BAC′等于（ ）
A、105° B、120° C、135° D、150°14. 关于x的一元二次方程x2+x+a2﹣1=0的一个根是0，则a的值为（ ）A、1 B、﹣1 C、1或﹣1 D、15. 制造一种产品，原来每件成本是100元，由于连续两次降低成本，现在的成本是81元，则平均每次降低的百分率是（ ）A、8.5% B、9% C、9.5% D、10%二、解答题：
-
16. 解方程：x（x﹣4）=2x﹣8．17. 求抛物线y=2x2﹣3x+1的顶点和对称轴．18. 已知二次函数图象经过点A（﹣3，0）、B（1，0）、C（0，﹣3），求此二次函数的解析式．
19. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC的顶点均在格点上，请按要求完成下列步骤：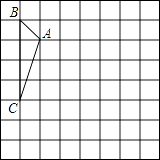
(1)、画出将△ABC向右平移3个单位后得到的△A1B1C1 ， 再画出将△A1B1C1绕点B1按逆时针方向旋转90°后所得到的△A2B1C2；(2)、求线段B1C1旋转到B1C2的过程中，点C1所经过的路径长．20.如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．
(1)、旋转中心是点 ， 旋转角度是度；(2)、若连结EF，则△AEF是三角形；并证明；(3)、若四边形AECF的面积为25，DE=2，求AE的长．21. 若x1、x2是方程x2+2（m﹣2）x+m2+4=0的两个实数根，且x12+x22﹣x1x2=21，求m的值．22. 已知二次函数y=﹣x2+2x+m．(1)、如果二次函数的图象与x轴有两个交点，求m的取值范围；(2)、如图，二次函数的图象过点A（3，0），与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．
23. 某商店经营儿童玩具，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是200件，而销售单价每上涨2元，月销售量就减少10件，但每件玩具售价不能高于40元．设每件玩具的销售单价上涨了x元时，月销售利润为y元．(1)、求y与x的函数关系式并直接写出自变量x的取值范围．(2)、每件玩具的售价定为多少元时，月销售利润恰为2280元？(3)、每件玩具的售价定为多少元时，月销售利润达到最大？最大为多少元？24.如图1，平面直角坐标系中，等腰直角三角形的直角边BC在x轴正半轴上滑动，点C的坐标为（t，0），直角边AC=4，经过O，C两点做抛物线y1=ax（x﹣t）（a为常数，a＞0），该抛物线与斜边AB交于点E，直线OA：y2=kx（k为常数，k＞0）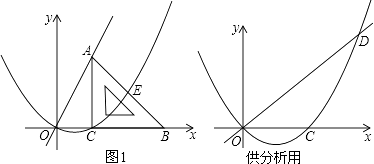
(1)、填空：用含t的代数式表示点A的坐标及k的值：A ， k=；(2)、随着三角板的滑动，当a= 时：①请你验证：抛物线y1=ax（x﹣t）的顶点在函数y= 的图象上；
②当三角板滑至点E为AB的中点时，求t的值；
(3)、直线OA与抛物线的另一个交点为点D，当t≤x≤t+4，|y2﹣y1|的值随x的增大而减小，当x≥t+4时，|y2﹣y1|的值随x的增大而增大，求a与t的关系式及t的取值范围．