2015-2016学年湖北省武汉市武昌区七校联考九年级上学期期中数学试卷

试卷更新日期：2016-11-09 类型：期中考试

进入出卷网下载

一、选择题

1. 方程3x²﹣4x﹣1=0的二次项系数和一次项系数分别为（）

A、3和4 B、3和﹣4 C、3和﹣1 D、3和1

查看试题解析
2. 二次函数y=x²﹣2x+2的顶点坐标是（）

A、（1，1） B、（2，2） C、（1，2） D、（1，3）

查看试题解析
3. 将△ABC绕O点顺时针旋转50°得△A₁B₁C₁（A、B分别对应A₁、B₁），则直线AB与直线A₁B₁的夹角（锐角）为（）

A、130° B、50° C、40° D、60°

查看试题解析
4. 用配方法解方程x²+6x+4=0，下列变形正确的是（　　）

A、（x+3）²=﹣4 B、（x﹣3）²=4 C、（x+3）²=5 D、（x+3）²=± $\sqrt{5}$

查看试题解析
5. 下列方程中没有实数根的是（）

A、x²﹣x﹣1=0 B、x²+3x+2=0 C、2015x²+11x﹣20=0 D、x²+x+2=0

查看试题解析
6. 平面直角坐标系内一点P（﹣2，3）关于原点对称的点的坐标是（）

A、（3，﹣2） B、（2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
7. 如图，⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC=3：5，则AB的长为（）

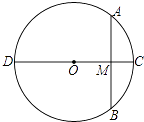A、 $\sqrt{91}$ cm B、8cm C、6cm D、4cm

查看试题解析
8. 已知抛物线C的解析式为y=ax²+bx+c，则下列说法中错误的是（）

A、a确定抛物线的形状与开口方向 B、若将抛物线C沿y轴平移，则a，b的值不变 C、若将抛物线C沿x轴平移，则a的值不变 D、若将抛物线C沿直线l：y=x+2平移，则a、b、c的值全变

查看试题解析
9.
如图，四边形ABCD的两条对角线互相垂直，AC+BD=16，则四边形ABCD的面积最大值是（）

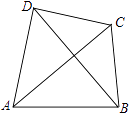A、64 B、16 C、24 D、32

查看试题解析
10. 已知二次函数的解析式为y=ax²+bx+c（a、b、c为常数，a≠0），且a²+ab+ac＜0，下列说法：
①b²﹣4ac＜0；
②ab+ac＜0；
③方程ax²+bx+c=0有两个不同根x₁、x₂ ，且（x₁﹣1）（1﹣x₂）＞0；
④二次函数的图象与坐标轴有三个不同交点，
其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 抛物线y=﹣x²﹣x﹣1的对称轴是．

查看试题解析
12. 已知x= $\frac{- b + \sqrt{b^{2} - 4 c}}{2}$ （b²﹣4c＞0），则x²+bx+c的值为．

查看试题解析
13. ⊙O的半径为13cm，AB，CD是⊙O的两条弦，AB∥CD，AB=24cm，CD=10cm．则AB和CD之间的距离．

查看试题解析
14.
如图，线段AB的长为1，C在AB上，D在AC上，且AC²=BC•AB，AD²=CD•AC，AE²=DE•AD，则AE的长为．

查看试题解析
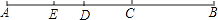15.
抛物线的部分图象如图所示，则当y＜0时，x的取值范围是．

查看试题解析
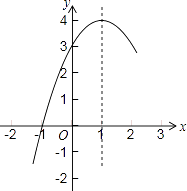16. 如图，△ABC是边长为a的等边三角形，将三角板的30°角的顶点与A重合，三角板30°角的两边与BC交于D、E两点，则DE长度的取值范围是．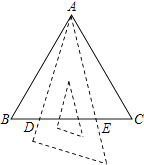

查看试题解析

三、解答题

17. 解方程：x²+x﹣2=0．

查看试题解析
18. 已知抛物线的顶点坐标是（3，﹣1），与y轴的交点是（0，﹣4），求这个二次函数的解析式．

查看试题解析
19. 已知x₁、x₂是方程x²﹣3x﹣5=0的两实数根

(1)、求x₁+x₂ ， x₁x₂的值；

(2)、求2x₁²+6x₂﹣2015的值．

查看试题解析
20. 如图所示，△ABC与点O在10×10的网格中的位置如图所示

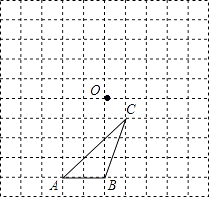(1)、画出△ABC绕点O逆时针旋转90°后的图形；

(2)、画出△ABC绕点O逆时针旋转180°后的图形；

(3)、若⊙M能盖住△ABC，则⊙M的半径最小值为多少？

查看试题解析
21. 如图，在⊙O中，半径OA垂直于弦BC，垂足为E，点D在CA的延长线上，若∠DAB+
∠AOB=60°

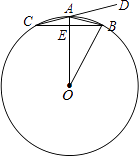(1)、求∠AOB的度数；

(2)、若AE=1，求BC的长．

查看试题解析
22. 飞机着陆后滑行的距离S（单位：m）关于滑行时间t（单位：s）的函数解析式是：S=60t﹣1.5t²

(1)、直接指出飞机着陆时的速度；

(2)、直接指出t的取值范围；

(3)、
画出函数S的图象并指出飞机着陆后滑行多远才能停下来？

查看试题解析
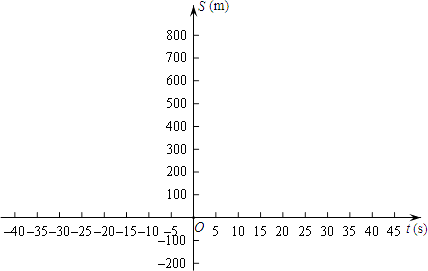23. 如图，△ABC是边长为6cm的等边三角形，点D从B点出发沿B→A方向在线段BA上以a cm/s速度运动，与此同时，点E从线段BC的某个端点出发，以b cm/s速度在线段BC上运动，当D到达A点后，D、E运动停止，运动时间为t（秒）

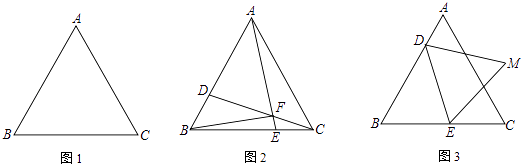(1)、如图1，若a=b=1，点E从C出发沿C→B方向运动，连AE、CD，AE、CD交于F，连BF．当0＜t＜6时：
①求∠AFC的度数；
②求 $\frac{A F^{2} + F C^{2} - B F^{2}}{A F \cdot F C}$ 的值；

(2)、如图2，若a=1，b=2，点E从B点出发沿B→C方向运动，E点到达C点后再沿C→B方向运动．当t≥3时，连DE，以DE为边作等边△DEM，使M、B在DE两侧，求M点所经历的路径长．

查看试题解析
24. 定义：我们把平面内与一个定点F和一条定直线l（l不经过点F）距离相等的点的轨迹（满足条件的所有点所组成的图形）叫做抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．

(1)、已知抛物线的焦点F（0， $\frac{1}{4 a}$ ），准线l： $y = - \frac{1}{4 a}$ ，求抛物线的解析式；

(2)、已知抛物线的解析式为：y=x²﹣n² ，点A（0， $\frac{1}{4} - n^{2}$ ）（n≠0），B（1，2﹣n²），P为抛物线上一点，求PA+PB的最小值及此时P点坐标；

(3)、若（2）中抛物线的顶点为C，抛物线与x轴的两个交点分别是D、E，过C、D、E三点作⊙M，⊙M上是否存在定点N？若存在，求出N点坐标并指出这样的定点N有几个；若不存在，请说明理由．

查看试题解析