2015-2016学年湖北省武汉市黄陂区九年级上学期期中数学试卷

试卷更新日期：2016-11-09 类型：期中考试

进入出卷网下载

一、选择题

1. 一元二次方程3x²﹣8x﹣10=0中的一次项系数为（）

A、3 B、8 C、﹣8 D、﹣10

查看试题解析
2. 如果﹣2是方程x²﹣m=0的一个根，则m的值为（）

A、2 B、﹣4 C、3 D、4

查看试题解析
3. 下列正多边形中，绕其中心旋转72°后，能和自身重合的是（）

A、正方形 B、正五边形 C、正六边形 D、正八边形

查看试题解析
4. 将二次函数y=x²的图象向下平移一个单位，则平移以后的二次函数的解析式为（）

A、y=x²﹣1 B、y=x²+1 C、y=（x﹣1）² D、y=（x+1）²

查看试题解析
5. 电脑病毒传播快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染，若每轮感染中平均一台电脑会感染x台电脑，下列方程正确的是（　）

A、x（x+1）=81 B、1+x+x²=81 C、1+x+x（x+1）=81 D、1+（x+1）²=81

查看试题解析
6. 一元二次方程x²+x﹣6=0的根的情况是（）

A、有两个相等的实根 B、没有实数根 C、有两个不相等的实根 D、无法确定

查看试题解析
7.
如图，在同一平面内，将△ABC绕点A旋转到△AED的位置，若AE⊥BC，∠ADC=65°，则∠ABC的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
8. 对于抛物线y=ax²﹣4ax+3a下列说法：①对称轴为x=2；②抛物线与x轴两交点的坐标分别为（1，0），（3，0）；③顶点坐标为（2，﹣a）；④若a＜0，当x＞2时，函数y随x的增大而增大，其中正确的结论有（）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9.
如图，矩形ABCD的两边BC、CD分别在x轴、y轴上，点C与原点重合，点A（﹣1，2），将矩形ABCD沿x轴向右翻滚，经过一次翻滚点A对应点记为A₁ ，经过第二次翻滚点A对应点记为A₂…依此类推，经过5次翻滚后点A对应点A₅的坐标为（）

A、（5，2） B、（6，0） C、（8，0） D、（8，1）

查看试题解析
10.
如图，等边△ABC的边长为3，F为BC边上的动点，FD⊥AB于D，FE⊥AC于E，则DE的长为（）

A、随F点运动，其值不变 B、随F点运动而变化，最大值为 $\frac{9}{4}$ C、随F点运动而变化，最小值为 $\frac{9}{4}$ D、随F点运动而变化，最小值为 $\frac{3}{2} \sqrt{3}$

查看试题解析

二、填空题

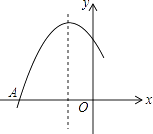
11. x²﹣6x+（）=（x﹣）²

查看试题解析
12. 二次函数y=x²﹣2x﹣3的图象的顶点坐标是．

查看试题解析
13. 若m、n是方程x²+6x﹣5=0的两根，则3m+3n﹣2mn= ．

查看试题解析
14.
如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（﹣3，0），该抛物线的对称轴为直线x=﹣1，若点C（﹣ $\frac{5}{2}$ ，y₁），D（﹣ $\frac{1}{2}$ ，y₂），E（ $\frac{3}{2}$ ，y₃）均为函数图象上的点，则y₁ ， y₂ ， y₃的大小关系为．

查看试题解析
15. 已知点C为线段AB上一点，且AC²=BC•AB，则 $\frac{A C}{A B}$ = ．

查看试题解析
16. 在△ABC中，AC=BC，∠ACB=90°，将△ABC绕点A旋转60°到△ADE的位置，点C的对应点为E，连接CD，若AC=BC=1，则CD的长为．

查看试题解析

三、解答题

17. 选择适当方法解方程：2x²﹣x﹣3=0．

查看试题解析
18. 已知关于x的方程x²﹣4x+1﹣p²=0．

(1)、若p=2，求原方程的根；

(2)、求证：无论p为何值，方程总有两个不相等的实数根．

查看试题解析
19. 已知抛物线y=ax²+bx+c过点A（﹣1，0），B（3，0），C（2，﹣ $\frac{3}{2}$ ）

(1)、求此抛物线的解析式；

(2)、当y＜0时，x的取值范围是（直接写出结果）

查看试题解析
20. 如图，线段AB两个端点的坐标分别为A（1，﹣1），B（3，1），将线段AB绕点O逆时针旋转90°到对应线段CD（点A与点C对应，点B与D对应）．

(1)、请在图中画出线段CD；

(2)、请直接写出点A、B的对应点坐标C（），D（）；

(3)、在x轴上求作一点P，使△PCD的周长最小，并直接写出点P的坐标（）．

查看试题解析
21.
如图，在△ABC中，AB=AC，点D为BC上一点，以AD为腰作等腰△ADE，AD=AE，∠BAC=∠DAE，连接CE．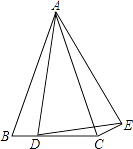

(1)、求证：BD=CE；

(2)、已知BC=8，∠BAC=∠DAE=30°，若△DCE的面积为1，求线段BD的长．

查看试题解析
22. 某宾馆有50个房间可供游客居住，当每个房间每天的定价为180元时，房间会全部住满，当每个房间每天的定价增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间的定价增加x元（x为10的整数倍），此时入住的房间数为y间，宾馆每天的利润为w元．

(1)、直接写出y（间）与x（元）之间的函数关系；

(2)、如何定价才能使宾馆每天的利润w（元）最大？

(3)、若宾馆每天的利润为10800元，则每个房间每天的定价为多少元？

查看试题解析
23.
如图，在正方形ABCD中，将正方形的边AD绕点A顺时针旋转到AE，连接BE、DE，过点A作AF⊥BE于F，交直线DE于P．

(1)、如图①，若∠DAE=40°，求∠P的度数；

(2)、如图②，若90°＜∠DAE＜180°，其它条件不变，试探究线段AP、DP、EP之间的数量关系，并说明理由；

(3)、继续旋转线段AD，若旋转角180°＜∠DAE＜270°，则线段AP、DP、EP之间的数量关系为（直接写出结果）

查看试题解析
24.
在平面直角坐标系中，抛物线C₁：y=ax²+4x+4a（0＜a＜2）

(1)、当C₁与x轴有唯一一个交点时，求此时C₁的解析式；

(2)、如图①，若A（1，y_A），B（0，y_B），C（﹣1，y_C）三点均在C₁上，连BC作AE∥BC交抛物线C₁于E，求点E到y轴的距离；

(3)、若a=1，将抛物线C₁先向右平移3个单位，再向下平移2个单位得到抛物线C₂ ，如图②，抛物线C₂与x轴相交于点M、N（M点在N点的左边），抛物线的对称轴交x轴于点F，过点F的直线l与抛物线C₂相交于P，Q（P在第四象限）且S_△_FMQ=2S_△_FNP ，求直线l的解析式．

查看试题解析