2015-2016学年山东省临沂市郯城县九年级上学期期末数学试卷
试卷更新日期:2016-11-09 类型:期末考试
一、选择题
-
1.
如图是一个三棱柱的立体图形,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球,则下列事件是必然事件的是( )A、摸出的四个球中至少有一个球是白球 B、摸出的四个球中至少有一个球是黑球 C、摸出的四个球中至少有两个球是黑球 D、摸出的四个球中至少有两个球是白球3. 如图,⊙O是△ABC的外接圆,连接OA、OB,∠OBA=50°,则∠C的度数为( )
2. 一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球,则下列事件是必然事件的是( )A、摸出的四个球中至少有一个球是白球 B、摸出的四个球中至少有一个球是黑球 C、摸出的四个球中至少有两个球是黑球 D、摸出的四个球中至少有两个球是白球3. 如图,⊙O是△ABC的外接圆,连接OA、OB,∠OBA=50°,则∠C的度数为( )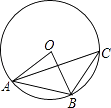 A、30° B、40° C、50° D、80°4. 已知反比例函数y= 的图象经过点P(﹣1,2),则这个函数的图象位于( )A、第二,三象限 B、第一,三象限 C、第三,四象限 D、第二,四象限5.
A、30° B、40° C、50° D、80°4. 已知反比例函数y= 的图象经过点P(﹣1,2),则这个函数的图象位于( )A、第二,三象限 B、第一,三象限 C、第三,四象限 D、第二,四象限5.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
 A、
A、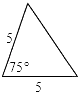 B、
B、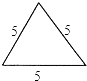 C、
C、 D、
D、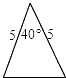 6. 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα= ,则t的值是( )
6. 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα= ,则t的值是( )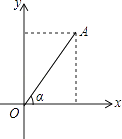 A、1 B、1.5 C、2 D、37.
A、1 B、1.5 C、2 D、37.如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高( )
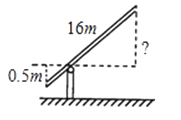 A、5m B、6m C、7m D、8m8.
A、5m B、6m C、7m D、8m8.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )
 A、55° B、60° C、65° D、80°9. 一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )A、cm B、cm C、3cm D、cm10.
A、55° B、60° C、65° D、80°9. 一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )A、cm B、cm C、3cm D、cm10.甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( )
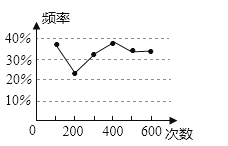 A、掷一枚正六面体的骰子,出现1点的概率 B、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率 C、抛一枚硬币,出现正面的概率 D、任意写一个整数,它能被2整除的概率11. 某方便面厂10月份生产方便面100吨,这样1至10月份生产量恰好完成全年的生产任务,为了满足市场需要,计划到年底再生产231吨方便面,这样就超额全年生产任务的21%,则11、12月的月平均增长率为( )A、10% B、31% C、13% D、11%12. 如图,在菱形ABCD中,DE⊥AB,cosA= ,BE=2,则BD的值( )
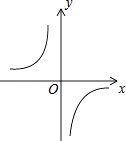
A、掷一枚正六面体的骰子,出现1点的概率 B、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率 C、抛一枚硬币,出现正面的概率 D、任意写一个整数,它能被2整除的概率11. 某方便面厂10月份生产方便面100吨,这样1至10月份生产量恰好完成全年的生产任务,为了满足市场需要,计划到年底再生产231吨方便面,这样就超额全年生产任务的21%,则11、12月的月平均增长率为( )A、10% B、31% C、13% D、11%12. 如图,在菱形ABCD中,DE⊥AB,cosA= ,BE=2,则BD的值( )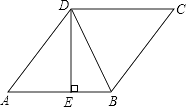 A、2 B、 C、2 D、513. 已知函数y= 的图象如图,以下结论:
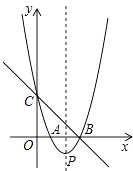
A、2 B、 C、2 D、513. 已知函数y= 的图象如图,以下结论:①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )
 A、4个 B、3个 C、2个 D、1个14.
A、4个 B、3个 C、2个 D、1个14.如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
 A、( , ) B、(2,2) C、( ,2) D、(2, )
A、( , ) B、(2,2) C、( ,2) D、(2, )二、填空题
-
15. 计算:sin30°+cos30°•tan60°= .16. 从地面竖直向上抛出一个小球,小球的高度h(米)与运动时间t(秒)之间的关系式为h=30t﹣5t2 , 那么小球抛出秒后达到最高点.17. 边长为1的正六边形的边心距是 .18. 如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y= (x<0)的图象经过点C,则k的值为 .
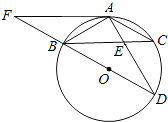
 19. 如图,在等边△ABC中,D为BC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为 .
19. 如图,在等边△ABC中,D为BC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为 .
三、解答题
-
20. 已知x=﹣2是关于x的方程2x2+ax﹣a2=0的一个根,求a的值.21. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.(1)、请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;(2)、求这两辆汽车都向左转的概率.22.
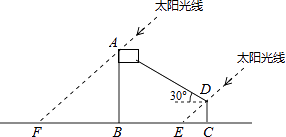
为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ≈1.414. ≈1.732)
 23. 在平面直角坐标系中,已知反比例函数y= 的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
23. 在平面直角坐标系中,已知反比例函数y= 的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°. (1)、试确定此反比例函数的解析式;(2)、将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.24.
(1)、试确定此反比例函数的解析式;(2)、将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.24.如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040)