2015-2016学年山东省临沂市平邑县九年级上学期期末数学试卷
试卷更新日期:2016-11-09 类型:期末考试
一、选择题
-
1. 一元二次方程x2﹣4=0的解是( )A、x1=2,x2=﹣2 B、x=﹣2 C、x=2 D、x1=2,x2=02. 抛物线y=2(x﹣3)2+1的顶点坐标是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)3. 点P(2,﹣3)关于原点对称的点的坐标是( )A、(﹣2,﹣3) B、(2,3) C、(﹣2,3) D、(﹣3,2)4. 已知圆的半径为3,一点到圆心的距离是5,则这点在( )A、圆内 B、圆上 C、圆外 D、都有可能5. 用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )A、(x﹣2)2=2 B、(x+2)2=2 C、(x﹣2)2=﹣2 D、(x﹣2)2=66. 一个布袋里装有6个只有颜色不同的球,其中2个红球,4个白球.从布袋里任意摸出1个球,则摸出的球是白球的概率为( )A、 B、 C、 D、7. 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
 A、116° B、32° C、58° D、64°8. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )
A、116° B、32° C、58° D、64°8. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )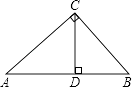 A、 B、 C、 D、9. 如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )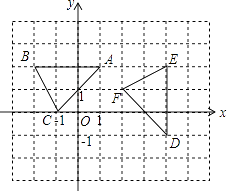 A、(0,0) B、(1,0) C、(1,﹣1) D、(2.5,0.5)10.
A、(0,0) B、(1,0) C、(1,﹣1) D、(2.5,0.5)10.如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
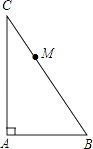 A、1条 B、2条 C、3条 D、4条11. 将抛物线y=x2﹣1向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )A、y=(x+2)2+1 B、y=(x﹣2)2﹣1 C、y=(x﹣2)2+1 D、y=(x+2)2﹣112. 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论是( )
A、1条 B、2条 C、3条 D、4条11. 将抛物线y=x2﹣1向左平移2个单位,再向上平移2个单位,得到的抛物线解析式为( )A、y=(x+2)2+1 B、y=(x﹣2)2﹣1 C、y=(x﹣2)2+1 D、y=(x+2)2﹣112. 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论是( ) A、②④ B、①③ C、②③ D、①④13. 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四种结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2 . 其中正确结论的序号是( )
A、②④ B、①③ C、②③ D、①④13. 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°.现给出以下四种结论:①∠A=45°;②AC=AB;③AE=BE;④CE•AB=2BD2 . 其中正确结论的序号是( ) A、①② B、②③ C、②④ D、③④14. 如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( )
A、①② B、②③ C、②④ D、③④14. 如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( ) A、
A、 B、
B、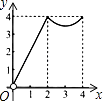 C、
C、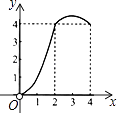 D、
D、
二、填空题
-
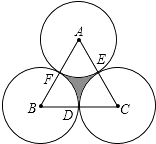
15. 在△ABC中,∠C=90°,cosA= ,则tanA等于 .16. 已知关于x的一元二次方程x2+2x﹣a=0有两个相等的实数根,则a的值是 .17. 如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为 .
 18. 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF分别交AC、CD于P、E,则图中的位似三角形共有对.
18. 如图,在平行四边形ABCD中,F是AD延长线上一点,连接BF分别交AC、CD于P、E,则图中的位似三角形共有对.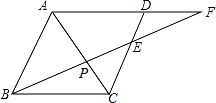 19. 如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥y轴,C、D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .
19. 如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥y轴,C、D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .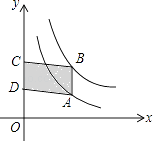
三、解答下列各题.
-
20. 计算与解方程(1)、计算: tan60°+|﹣3sin30°|﹣cos245°.(2)、解方程:x2+4x+1=0.21. 某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有121台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过1300台?22. 如图,一次函数y1=kx+b的图象与反比例函数y2= (x>0)的图象交于A(1,6),B(a,2)两点.
 (1)、求一次函数与反比例函数的解析式;(2)、直接写出y1≤y2时x的取值范围.23. 如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.求证:
(1)、求一次函数与反比例函数的解析式;(2)、直接写出y1≤y2时x的取值范围.23. 如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.求证: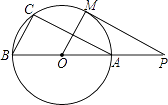 (1)、△ABC∽△POM;(2)、2OA2=OP•BC.24. 如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°.
(1)、△ABC∽△POM;(2)、2OA2=OP•BC.24. 如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°. (1)、判断CD与⊙O的位置关系,并说明理由;(2)、若⊙O半径为6cm,AE=10cm,求∠ADE的正弦值.25. 矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
(1)、判断CD与⊙O的位置关系,并说明理由;(2)、若⊙O半径为6cm,AE=10cm,求∠ADE的正弦值.25. 矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.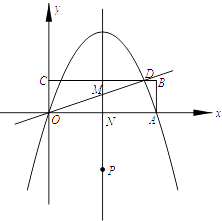 (1)、求抛物线的解析式;(2)、连接AD,试判断△OAD的形状,并说明理由.(3)、若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、连接AD,试判断△OAD的形状,并说明理由.(3)、若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由.