2015-2016学年山东省济宁市汶上县九年级上学期期末数学试卷

试卷更新日期：2016-11-09 类型：期末考试

进入出卷网下载

一、选择题

1. 若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
2. 对于一般的二次函数y=x²+bx+c，经过配方可化为y=（x﹣1）²+2，则b，c的值分别为（）

A、5，﹣1 B、2，3 C、﹣2，3 D、﹣2，﹣3

查看试题解析
3. 如图，AB是⊙O的直径，C、D是⊙O上一点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于（）

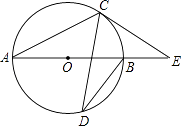A、40° B、50° C、60° D、70°

查看试题解析
4. 已知⊙O半径为3，M为直线AB上一点，若MO=3，则直线AB与⊙O的位置关系为（　　）

A、相切 B、相交 C、相切或相离 D、相切或相交

查看试题解析
5. 对于函数y= $\frac{4}{x}$ ，下列说法错误的是（）

A、这个函数的图象位于第一、第三象限 B、当x＞0时，y随x的增大而增大 C、这个函数的图象既是轴对称图形又是中心对称图形 D、当x＜0时，y随x的增大而减小

查看试题解析
6. 如图，菱形ABCD的对角线相交于坐标原点，点A的坐标为（a，2），点B的坐标为（﹣1，﹣ $\sqrt{3}$ ），点C的坐标为（2 $\sqrt{3}$ ，c），那么a，c的值分别是（）

A、a=﹣1，c=﹣ $\sqrt{3}$ B、a=﹣2 $\sqrt{3}$ ，c=﹣2 C、a=1，c= $\sqrt{3}$ D、a=2 $\sqrt{3}$ ，c=2

查看试题解析
7.
已知抛物线y=ax²+b（a≠0）在平面直角坐标系中的位置如图所示，那么一元二次方程ax²﹣x+b=0根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
8. 如图所示：抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=1，且经过点（﹣1，0），康康依据图象写出了四个结论：
①如果点（﹣ $\frac{1}{2}$ ，y₁）和（2，y₂）都在抛物线上，那么y₁＜y₂；
②b²﹣4ac＞0；
③m（am+b）＜a+b（m≠1的实数）；
④ $\frac{c}{a}$ =﹣3．
康康所写的四个结论中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9.
把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形，如果所剪得的两个正方形边长都是1，那么圆形纸片和扇形纸片的面积比是（）

A、4：5 B、2：5 C、 $\sqrt{5}$ ：2 D、 $\sqrt{5}$ ： $\sqrt{2}$

查看试题解析

二、填空题

10. 已知x=﹣1是一元二次方程ax²+bx﹣2=0的一个根，那么b﹣a的值等于．

查看试题解析
11. 函数 $y = (m - 1) x^{m^{2} + 1} - 2 m x + 1$ 的图象是抛物线，则m= ．

查看试题解析
12.
在纸上剪下一个圆和一个扇形纸片，使它们恰好围成一个圆锥（如图所示），如果扇形的圆心角为90°，扇形的半径为8，那么所围成的圆锥的高为．

查看试题解析
13.
如图，点E在正方形ABCD的边CD上，把△ADE绕点A顺时针旋转90°至△ABF位置，如果AB= $\sqrt{3}$ ，∠EAD=30°，那么点E与点F之间的距离等于．

查看试题解析
14.
如果两个圆只有一个公共点，那么我们称这两个圆相切，这个公共点就叫做切点，当两圆相切时，如果其中一个圆（除切点外）在另一个圆的内部，叫做这两个圆内切；其中一个圆（除切点外）在另一个圆的外部，叫做这两个圆外切．如图所示：两圆的半径分别为R，r（R＞r），两圆的圆心之间的距离为d，若两个圆外切则d=R+r，若两个圆内切则d=R﹣r，已知两圆的半径分别为方程x²+mx+3=0的两个根，当两圆相切时，已知这两个圆的圆心之间的距离为4，则m的值为．

查看试题解析

三、解答题

15. 用规定的方法解方程：

(1)、x²﹣x﹣2=0；（公式法）

(2)、x²﹣7=﹣6x．（配方法）

查看试题解析
16. 小青和小白在一起玩数学游戏，他们约定：在一个不透明的布袋中有四个完全相同的小球，把它们分别标号为1，2，3，4，小青随机摸出一个小球记下数字后放回去，小白再随机摸出一个小球记下数字．

(1)、求小青和小白摸出小球标号相同的概率；

(2)、如果小青和小白按照上述方式继续进行游戏，并且把他们所摸出的两个数分别看作点的横坐标和纵坐标，记作（小青，小白），当点在直线y=x+1上时，小青胜；反之则小白胜，请判断这个游戏对双方是否公平，并说明理由．

查看试题解析
17.
如图，在平面直角坐标系网格中，△ABC的顶点都在格点上，点C坐标（0，﹣1）．

(1)、作出△ABC关于原点对称的△A₁B₁C₁ ，并写出点A₁的坐标；

(2)、把△ABC绕点C逆时针旋转90°，得△A₂B₂C，画出△A₂B₂C，并写出点A₂的坐标；

(3)、直接写出△A₂B₂C的面积．

查看试题解析
18.
已知，如图，AB是⊙O的直径，C为⊙O上一点，AD垂直于经过点C的直线DE，垂足为点D，AC平分∠DAB．

(1)、求证：直线DE是⊙O的切线；

(2)、连接BC，猜想：∠ECB与∠CAB的数量关系，并证明你的猜想．

查看试题解析
19.
如图，已知一次函数y=x+b与反比例函数y= $\frac{k}{x}$ 的图象交于A、B两点，其中点A的坐标为（2，3）．

(1)、求一次函数与反比例函数的解析式；

(2)、求点B的坐标；

(3)、请根据图象直接写出不等式x+b＞ $\frac{k}{x}$ 的解集．

查看试题解析
20. 九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件）
100
110
120
130
…
月销量（件）
200
180
160
140
…
已知该运动服的进价为每件60元，设售价为x元．

(1)、请用含x的式子表示：
①销售该运动服每件的利润是（）元；
②月销量是（）件；（直接写出结果）

(2)、设销售该运动服的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？

(3)、若销售该运动服所得的月利润不低于8000元，请确定售价x的取值范围．

查看试题解析
21.
如图，直线y₁=﹣ $\frac{1}{2}$ x+2与x轴，y轴分别交于B，C，抛物线y=ax²+bx+c（a≠0）经过点A，B，C，点A坐标为（﹣1，0）．

(1)、求抛物线的解析式；

(2)、抛物线的对称轴与x轴交于点D，连接CD，点P是直线BC上方抛物线上的一动点（不与B，C重合），当点P运动到何处时，四边形PCDB的面积最大？求出此时四边形PCDB面积的最大值和点P坐标；

(3)、在抛物线上的对称轴上是否存在一点Q，使△QCD是以CD为腰的等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析

售价（元/件）	100	110	120	130	…
月销量（件）	200	180	160	140	…