2015-2016学年湖北省孝感市应城市九年级上学期期末数学试卷

试卷更新日期：2016-11-09 类型：期末考试

进入出卷网下载

一、选择题

1. 下列交通标志中既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程x²﹣9=0的根是（　　）

A、x=﹣3 B、x₁=3，x₂=﹣3 C、x₁=x₂=3 D、x=3

查看试题解析
3. 把抛物线y=（x﹣1）²+2向左平移1个单位，再向下平移2个单位，所得抛物线是（）

A、y=x² B、y=（x﹣2）² C、y=（x﹣2）²+4 D、y=x²+4

查看试题解析
4. 下列说法：
①三点确定一个圆；
②垂直于弦的直径平分弦；
③三角形的内心到三条边的距离相等；
④圆的切线垂直于经过切点的半径．
其中正确的个数是（）

A、0 B、2 C、3 D、4

查看试题解析
5. 如图，底边长为2的等腰Rt△ABO的边OB在x轴上，将△ABO绕原点O逆时针旋转45°得到△OA₁B₁ ，则点A₁的坐标为（）

A、（1，﹣ $\sqrt{2}$ ） B、（1，﹣1） C、（ $\sqrt{2} ， - \sqrt{2}$ ） D、（ $\sqrt{2}$ ，﹣1）

查看试题解析
6. 如图，点A、C、B在⊙O上，已知∠AOB=∠ACB=α．则α的值为（）

A、135° B、120° C、110° D、100°

查看试题解析
7. 如图，⊙O的半径为5，点O到直线l的距离为7，点P是直线l上的一个动点，PQ与⊙O相切于点Q，则PQ的最小值为（）

A、 $\sqrt{17}$ B、 $\sqrt{5}$ C、2 $\sqrt{6}$ D、2

查看试题解析
8. 关于x的函数y=k（x+1）和y= $\frac{k}{x}$ （k≠0）在同一坐标系中的图象大致是（）

A、 B、 C、 D、

查看试题解析
9. 若A（3，y₁），B（5，y₂），C（﹣2，y₃）是抛物线y=﹣x²+4x+k上的三点，则y₁、y₂、y₃的大小关系为（）

A、y₂＞y₁＞y₃ B、y₃＞y₂＞y₁ C、y₁＞y₂＞y₃ D、y₃＞y₁＞y₂

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x=2，下列结论：
①4a+b=0；
②9a+c＜3b；
③25a+5b+c=0；
④当x＞2时，y随x的增大而减小．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：每小题3分，共18分．

11. 用配方法解方程x²﹣2x﹣7=0时，配方后的形式为．

查看试题解析
12. 如图，把△ABC绕点A逆时针旋转42°，得到△AB′C′，点C′恰好落在边AB上，连接BB′，则∠B′BC′的大小为．

查看试题解析
13. 如图，点P在反比例函数y= $\frac{k}{x}$ （x＜0）的图象上，PA⊥x轴于点A，△PAO的面积为5，则k的值为．

查看试题解析
14. 将半径为5的圆形纸片，按如图方式折叠，若 $\overset{⌢}{A B}$ 和 $\overset{⌢}{B C}$ 都经过圆心O，则图中阴影部分的面积是．

查看试题解析
15. 如图，一次函数y₁=k₁+b与反比例函数y₂= $\frac{k_{2}}{x}$ 的图象相交于A（﹣1，2）、B（2，﹣1）两点，则y₂＜y₁时，x的取值范围是．

查看试题解析
16. 如图，直线y=x﹣4与x轴、y轴分别交于M、N两点，⊙O的半径为2，将⊙O以每秒1个单位的速度向右作平移运动，当移动时间秒时，直线MN恰好与圆相切．

查看试题解析

三、解答题：共72分，解答应写出文字说明、证明过程或演算步骤．

17. 解下列方程：

(1)、x²﹣2x﹣3=0；

(2)、（x﹣5）²=2（5﹣x）

查看试题解析
18. 如图，等腰Rt△ABC中，BA=BC，∠ABC=90°，点D在AC上，将△ABD绕点B沿顺时针方向旋转90°后，得到△CBE．

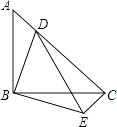(1)、求∠DCE的度数；

(2)、若AB=4，CD=3AD，求DE的长．

查看试题解析
19. 如图，在平面直角坐标系中，已知点A（1，3）、B（3，3）、C（4，2）．

(1)、请在图中作出经过点A、B、C三点的⊙M，并写出圆心M的坐标；

(2)、若D（1，4），则直线BD与⊙M ．

A、相切 B、相交．

查看试题解析
20. 在一个暗箱中装有红、黄、白三种颜色的乒乓球（除颜色外其余均相同），其中白球、黄球各1个，且从中随机摸出一个球是白球的概率是 $\frac{1}{4}$ ．

(1)、求暗箱中红球的个数；

(2)、先从暗箱中随机摸出一个球，记下颜色放回，再从暗箱中随机摸出一个球，求两次摸到的球颜色不同的概率．

查看试题解析
21. 已知关于x的方程x²﹣2（k+1）x+k²=0有两个实数根x₁、x₂ ．

(1)、求k的取值范围；

(2)、若x₁+x₂=3x₁x₂﹣6，求k的值．

查看试题解析
22. 如图，⊙O是△ABC的外接圆，圆心O在AB上，M是OA上一点，过M作AB的垂线交BC的延长线于点E，过点C作⊙O的切线，交ME于点F．

(1)、求证：EF=CF；

(2)、若∠B=2∠A，AB=4，且AC=CE，求BM的长．

查看试题解析
23. 某大学毕业生响应国家“自主创业”的号召，投资开办了一个装饰品商店，该店购进一种新上市的饰品进行了30天的试销售，购进价格为40元/件．销售结束后，得知日销售量P（件）与销售时间x（天）之间有如下关系：P=﹣2x+120（1≤x≤30，且x为整数）；销售价格Q（元/件）与销售时间x（天）之间有如下关系：Q= $\frac{1}{2}$ x+50（1≤x≤30，且x为整数）．

(1)、试求出该商店日销售利润w（元）与销售时间x（天）之间的函数关系式；

(2)、在这30天的试销售中，哪一天的日销售利润最大，哪一天的日销售利润最小？并分别求出这个最大利润和最小利润．

查看试题解析
24. 如图，已知抛物线y=ax²+bx+c（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．

(1)、求此抛物线的解析式；

(2)、若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；

(3)、点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．

查看试题解析