山东省烟台市龙口市2015-2016学年七年级上学期数学期末考试试卷
试卷更新日期:2018-02-09 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列四个数中,无理数是( )
2. 下列四个数中,无理数是( )
A、 B、0.5 C、0 D、π3. 下列各点中,在第二象限的点是( )
A、(﹣3,2) B、(﹣3,﹣2) C、(3,2) D、(3,﹣2)4. 若实数a>0,b<0,则函数y=ax+b的图象可能是( )A、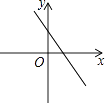 B、
B、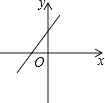 C、
C、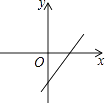 D、
D、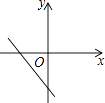 5. 的平方根是( )A、±4 B、4 C、±2 D、26. 将平面直角坐标系内某图形上各个点的纵坐标都乘以﹣1,横坐标不变,所得图形与原图形的关系是( )
5. 的平方根是( )A、±4 B、4 C、±2 D、26. 将平面直角坐标系内某图形上各个点的纵坐标都乘以﹣1,横坐标不变,所得图形与原图形的关系是( )
A、关于y轴对称 B、关于x轴对称 C、沿x轴向左平移1个单位长度 D、沿y轴向下平移1个单位长度7. 已知三角形的两边长分别为4cm和7cm,则此三角形的第三边长可能是( )
A、3cm B、11cm C、7cm D、15cm8. 如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )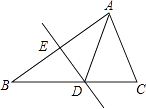 A、7cm B、10cm C、12cm D、22cm9. 如图所示,AB=BC=CD=DE=1,AB⊥BC , AC⊥CD , AD⊥DE , 则AE=( )
A、7cm B、10cm C、12cm D、22cm9. 如图所示,AB=BC=CD=DE=1,AB⊥BC , AC⊥CD , AD⊥DE , 则AE=( ) A、1 B、 C、 D、210. 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可以证明△EDC≌△ABC,得到ED=AB,因此测得ED的长就是AB的长(如图),判定△EDC≌△ABC的理由是( )
A、1 B、 C、 D、210. 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可以证明△EDC≌△ABC,得到ED=AB,因此测得ED的长就是AB的长(如图),判定△EDC≌△ABC的理由是( )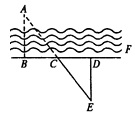 A、SAS B、ASA; C、SSS D、HL11. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
A、SAS B、ASA; C、SSS D、HL11. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.
 A、4 B、3 C、2 D、112. 如图是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在要从其余13个白色小方格中选出一个也涂成黑色的图形称为轴对称图形,这样的白色小方格有( )
A、4 B、3 C、2 D、112. 如图是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在要从其余13个白色小方格中选出一个也涂成黑色的图形称为轴对称图形,这样的白色小方格有( )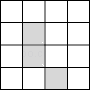 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
13. 若用初中数学课本上使用的科学计算器进行计算,则以下按键的结果为 .
 14. 估算 =(误差小于0.1).
14. 估算 =(误差小于0.1).
15. 点P(x,y)是第一象限的一个动点,且满足x+y=10,点A(8,0).若△OPA的面积为S,则S关于x的函数解析式为 .16. 如图是某校的平面示意图,如果分别用(3,﹣1)、(﹣3,2)表示图中图书馆和实验楼的位置,那么校门的位置可表示为 .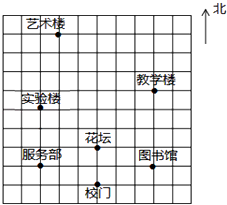 17. 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 .
17. 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 .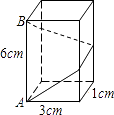 18. 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .
18. 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .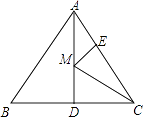 19. 已知7﹣2a的平方根是± , 2是b的算术平方根,求ab的立方根.
19. 已知7﹣2a的平方根是± , 2是b的算术平方根,求ab的立方根.三、解答题
-
20. 计算: ﹣( )2+ .
21. 在8×8的方格纸中,设小方格的边长为1.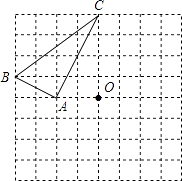 (1)、请判断△ABC的形状并说明理由.
(1)、请判断△ABC的形状并说明理由.
(2)、画出△ABC以CO所在直线为对称轴的对称图形△A′B′C′,并在所画图中标明字母.
22. 已知一次函数y=mx﹣3m2+12,请按要求解答问题:
(1)、m为何值时,函数图象过原点,且y随x的增大而减小?
(2)、若函数图象平行于直线y=﹣x,求一次函数解析式;
(3)、若点(0,﹣15)在函数图象上,求m的值.
23. 在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)、如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;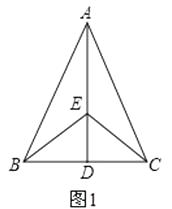 (2)、如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.
(2)、如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.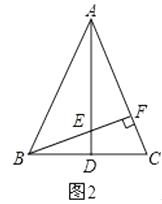 24. 某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
24. 某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.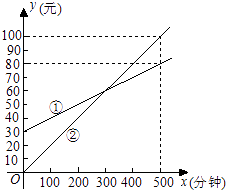 (1)、有月租费的收费方式是(填①或②),月租费是元;(2)、分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(1)、有月租费的收费方式是(填①或②),月租费是元;(2)、分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)、请你根据用户通讯时间的多少,给出经济实惠的选择建议.25. 如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方? 26. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?
26. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?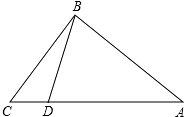 27. 如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
27. 如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.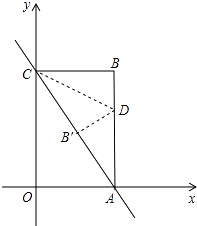 (1)、求点A、C的坐标;(2)、将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(1)、求点A、C的坐标;(2)、将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)、在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.