山东省威海市乳山市2015-2016学年七年级上学期数学期末考试试卷
试卷更新日期：2018-02-09 类型：期末考试
一、单选题
-
1. 下列结论正确的是（ ）A、 =﹣2 B、 =﹣2 C、 =±2 D、 =±22. 下列几组数能作为直角三角形的三边长的是（ ）
A、2，2， B、 ，2， C、9，12，18 D、12，15，203. 通过估算比较大小，下列结论不正确的是（ ）
A、 B、﹣ ＞ C、 D、4. 已知点（﹣3，y1），（1，y2）都在直线y=kx+2（k＜0）上，则y1 ， y2大小关系是（ ）A、y1＞y2 B、y1=y2 C、y1＜y2 D、不能比较5. 如图，AB=AC，添加下列条件，不能使△ABE≌△ACD的是（ ）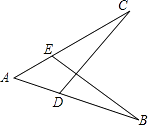
A、∠B=∠C B、∠AEB=∠ADC C、AE=AD D、BE=DC6. 如图，在△ABC中，∠B=30°，ED垂直平分BC，若BC=6，则BE=（ ）
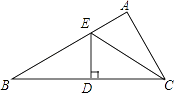A、2 B、3 C、 D、67. 如图是中国象棋棋盘的一部分，若
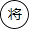位于点（1，﹣1），则 
位于点（ ）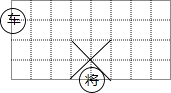
A、（3，﹣2） B、（2，﹣3） C、（﹣2，3） D、（﹣3，2）8. 关于一次函数y=2x﹣1，y=﹣2x+1的图象，下列说法正确的是（ ）A、关于直线y=﹣x对称 B、关于x轴对称 C、关于y轴对称 D、关于直线y=x对称9. 如图为正方形网格，则∠1+∠2+∠3=（ ）
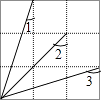A、105° B、120° C、115° D、135°10. 如图，直线l是一次函数y=kx+b的图象，当﹣1＜x＜0时，y的取值范围是（ ）
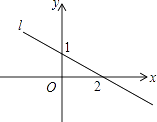A、1＜y＜ B、 ＜y＜1 C、y＞1 D、0＜y11.如图，网格中的每个小正方形的边长为1，A，B是格点，则以A，B，C为等腰三角形顶点的所有格点C的位置有（ ）
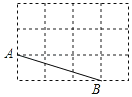A、2个 B、3个 C、4个 D、5个12. 如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，BE=4，则AD的长是（ ）
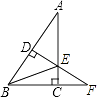A、4 B、2 C、6 D、2二、填空题
-
13. 52的平方根是 ．
14. 已知 与 互为相反数，则ab的值为 ．
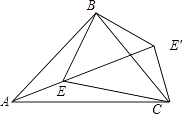
15. 如图，AB∥EF，∠C=∠D=85°，CF=BD，若∠A=40°，则∠EFD= ．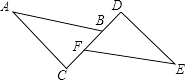
16. 若一次函数y=kx+b的图象沿y轴向上平移3个单位后，得到图象的关系式是y=2x+2，则原一次函数的关系式为 ．
17. 已知点P的坐标为（1+a，2a﹣2），且点P到两坐标轴的距离相等，则a的值是 ．18. 如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在D′处，若AB=3，AD=4，则S△CED′：S△CEA= ．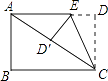
三、解答题
-
19. 计算： ﹣ + +| |（精确到0.01）20. 如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0）、（﹣3，1），AB=AC．
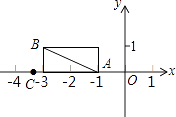(1)、求点C的坐标；
(2)、比较点C的横坐标与﹣3.3的大小．
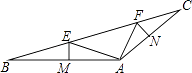
21. 如图，△ABC是等边三角形，D是AC上一点，BD=CE，∠1=∠2，试判断BC与AE的位置关系，并证明你的结论．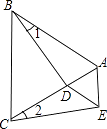
22. 利群超市经销某品牌童装，单价为每件40元时，每天销量为60件，当从单价每件40元降了20元时，一天销量为100件，设降x元时，一天的销量为y千克．已知y是x的一次函数．
(1)、求y与x之间的关系式；
(2)、若某天销售童装80件，则该天童装的单价是多少？
23. 某通讯公司推出①、②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间的函数关系如图所示．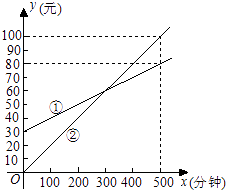
(1)、有月租费的收费方式是（填①或②），月租费是元；(2)、分别求出①、②两种收费方式中y与自变量x之间的函数关系式；
(3)、请你根据用户通讯时间的多少，给出经济实惠的选择建议．
