山东省日照市五莲县2015-2016学年七年级上学期数学期末考试试卷
试卷更新日期：2018-02-09 类型：期末考试
一、单选题
-
1. |﹣2010|倒数的相反数是（ ）A、2010 B、﹣2010 C、 D、-2. 2013年12月15日，嫦娥三号着陆器、巡视器顺利完成互拍，把成像从远在地球38万km之外的月球传到地面，标志着我国探月工程二期取得圆满成功，将38万用科学记数法表示应为（ ）
A、0.38×106 B、0.38×105 C、3.8×104 D、3.8×1053.有理数a，b在数轴上对应点的位置如图所示，下列各式正确的是（ ）
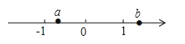A、a+b＜0 B、a﹣b＜0 C、a•b＞0 D、＞04. 关于x的方程（a﹣1）x2+x+a2﹣4=0是一元一次方程，则方程的解为（ ）A、1 B、2 C、3 D、﹣25. 如图是每个面上都有一个汉字的正方体的一种平面展开图，那么在原正方体中和“国”字相对的面是（ ）
A、中 B、钓 C、鱼 D、岛6. 下列说法中，正确的有（ ）个①过两点有且只有一条直线 ②连接两点的线段叫做两点间的距离
③两点之间，线段最短 ④若AB=BC，则点B是线段AC的中点
⑤射线AB和射线BA是同一条射线 ⑥直线有无数个端点．
A、2个 B、3个 C、4个 D、5个7. 如图，点C是线段AB上一点，点M是AC的中点，点N是BC的中点，如果MC比NC长3cm，AC比BC长（ ）
A、6cm B、4cm C、3cm D、1.5cm8. 由3点15分到3点30分，时钟的分针转过的角度是（ ）A、90° B、60° C、45° D、30°9. 在式子 ，﹣ 中，单项式的个数是（ ）A、5个 B、4个 C、3个 D、2个10. 如果x=y，a为有理数，那么下列等式不一定成立的是（ ）A、4﹣y=4﹣x B、x2=y2 C、 D、﹣2ax=﹣2ay11. 按如图所示的程序计算：若开始输入的x值为﹣2，则最后输出的结果是（ ）
A、352 B、160 C、112 D、19812. 如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③ （∠α+∠β）；④ （∠α﹣∠β）．正确的有（ ）
A、4个 B、3个 C、2个 D、1个13. 当k=时，多项式x2﹣（k﹣3）xy﹣3y2+2xy﹣5中不含xy项．14. 已知：如图，点D是AB的中点，BC= ，DC=2，则AB的长为 ．
15. 若a2﹣3b=2，则6b﹣2a2+2015= ．16. 观察下面的一列单项式：﹣2x、4x3、﹣8x5、16x7、…根据你发现的规律，第n个单项式为 ．17.
(1)、计算：﹣24(2)、解方程：(3)、已知：A=x2﹣5x，B=3x2+2x﹣6，求3A﹣B的值，其中x=﹣2．
18. 已知：如图所示，∠AOB：∠BOC=3：2，OD平分∠BOC，OE平分∠AOC，且∠DOE=36°，求∠BOE的度数．
19. 一项工程，如果由甲单独做，需要12小时完成；如果由乙单独做，需要15小时完成．甲先做3小时，剩下的工程由甲乙合作完成，则在完成此项工程中，甲一共干了多少小时？20. 如图，OM是∠AOC的平分线，ON是∠BOC的平分线．(1)、如图1，当∠AOB是直角，∠BOC=60°时，∠MON的度数是多少？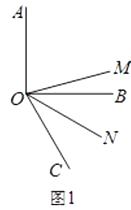
(2)、如图2，当∠AOB=α，∠BOC=60°时，猜想∠MON与α的数量关系；
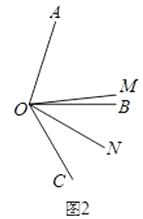(3)、如图3，当∠AOB=α，∠BOC=β时，猜想∠MON与α、β有数量关系吗？如果有，指出结论并说明理由．
21. 列方程解应用题：五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的 倍多15件，甲、乙两种商品的进价和售价如下表（注：获利=售价﹣进价）甲
乙
进价（元/件）
20
30
售价（元/件）
29
40
(1)、新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？(2)、该购物中心第二次以第一次的进价又购进甲、乙两种商品，其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元，求第二次乙种商品是按原价打几折销售？22. 如图
(1)、若点P为AB的中点，直接写出点P对应的数；(2)、数轴的原点右侧是否存在点P，使点P到点A、点B的距离之和为8？若存在，请求出x的值；若不存在，说明理由；(3)、现在点A、点B分别以每秒2个单位长度和每秒0.5个单位长度的速度同时向右运动，同时点P以每秒6个单位长度的速度从表示数1的点向左运动．当点A与点B之间的距离为3个单位长度时，求点P所对应的数是多少？