2017-2018学年人教版数学八年级下册同步训练： 18.1.2《平行四边形的判定》
试卷更新日期：2018-02-09 类型：同步测试
一、选择题
-
1. 下面给出了四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能判定四边形ABCD是平行四边形的是（ ）A、1：2：3：4 B、2：2：3：3 C、2：3：2：3 D、2：3：3：2．2. 能判定四边形ABCD为平行四边形的题设是（）．A、AB∥CD，AD＝BC B、∠A＝∠B，∠C＝∠D C、AB＝CD，AD＝BC D、AB＝AD，CB＝CD3. 下面给出的条件中，能判定一个四边形是平行四边形的是（ ）A、一组对边平行，另一组对边相等 B、一组对边平行，一组对角互补 C、一组对角相等，一组邻角互补 D、一组对角相等，另一组对角互补4. 列条件中能判断四边形是平行四边形的是（）．A、对角线互相垂直 B、对角线相等 C、对角线互相垂直且相等 D、对角线互相平分5. 如图，有两块全等的含30°角的三角板拼成形状不同的平行四边形，最多可以拼成（ ）
A、1个 B、2个 C、3个 D、4个6. A，B，C，D在同一平面内，从①AB∥CD，②AB=CD，③BC∥AD，④BC=AD这四个中任选两个作为条件，能使四边形ABCD为平行四边形的选法有（ ）A、6种 B、5种 C、4种 D、3种7. 能判定四边形是平行四边形的条件是（ ）A、一组对边平行，另一组对边相等 B、一组对边相等，一组邻角相等 C、一组对边平行，一组邻角相等 D、一组对边平行，一组对角相等8. 已知四边形ABCD，AC与BD相交于点O，如果给出条件AB∥CD，那么还不能判定四边形ABCD为平行四边形，以下四种说法正确的是（ ）①如果再加上条件BC=AD，那么四边形ABCD一定是平行四边形；
②如果再加上条件∠BAD=∠BCD，那么四边形ABCD一定是平行四边形；
③如果再加上条件AO=CO，那么四边形ABCD一定是平行四边形；
④如果再加上条件∠DBA=∠CAB，那么四边形ABCD一定是平行四边形．
A、①② B、①③④ C、②③ D、②③④9. 已知四边形ABCD的对角线相交于O，给出下列5个条件①AB∥CD；②AD∥BC；③AB=CD；④∠BAD=∠DCB．从以上4个条件中任选2个条件为一组，能推出四边形ABCD为平行四边形的有（ ）A、6组 B、5组 C、4组 D、3组10. 在四边形ABCD中，从①AB∥CD；②AB=CD；③BC∥AD；④BC=AD中任选两个使四边形ABCD为平行四边形的选法有（ ）A、3 B、4 C、5 D、611. 四边形ABCD中，AD∥BC，当满足下列条件时，四边形ABCD是平行四边形的是（ ）．A、∠A+∠C=180° B、∠B+∠D=180° C、∠A+∠B=180° D、∠A+∠D=180°12. 以不在同一直线上的三个点为顶点作平行四边形，最多能作（ ）A、4个 B、3个 C、2个 D、1个13. 在下列给出的条件中，能判定四边形ABCD为平行四边形的是（ ）A、AB=BC，CD=DA B、AB∥CD，AD=BC C、AB∥CD，∠A=∠C D、∠A=∠B，∠C=∠D14. 下列哪组条件能判别四边形ABCD是平行四边形（ ）A、AB∥CD，AD=BC B、AB=CD，AD=BC C、∠A=∠B，∠C=∠D D、AB=AD，CB=CD15. 如图所示，在△ABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AFDE的周长是（ ）
A、5 B、10 C、15 D、20二、填空题
-
16. 如图，在四边形ABCD中，AC、BD相交于点O，
(1)、若AB＝4cm，AD＝8cm，当BC＝cm，CD＝cm时，四边形ABCD为平行四边形；(2)、若BD＝8cm，AC＝10cm，当AO＝cm，DO＝cm时，四边形ABCD为平行四边形．17. 如图，四边形ABCD中，AB∥CD，要使四边形ABCD为平行四边形，则应添加的条件是 ． （添加一个条件即可，不添加其它的点和线）．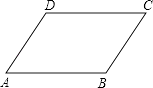
18. 如图，在四边形ABCD中，已知AB=CD，再添加一个条件（写出一个即可），则四边形ABCD是平行四边形．（图形中不再添加辅助线）19. 如图，△ABC，△ACE，△ECD都是等边三角形，则图中的平行四边形有哪些 ．
20. 把边长为3，5，7的两个全等三角形拼成四边形，一共能拼成种不同的四边形，其中有个平行四边形．三、解答题
-
21. 已知：如图，在平行四边形ABCD中，E，F分别是AB，DC上的两点，且AE＝CF．求证：BD，EF互相平分.
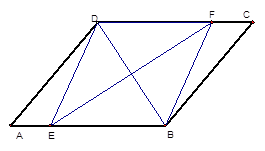22. 如图，E，F是四边形ABCD的对角线AC上两点，AF=CE，DF=BE，DF∥BE．求证：
(1)、△AFD≌△CEB；(2)、四边形ABCD是平行四边形．
