河北省沧州市2015-2016学年七年级上学期数学期末考试试卷
试卷更新日期:2018-02-09 类型:期末考试
一、单选题
-
1. 若向东走5m,记为+5m,则﹣3m表示为( )A、向东走3m B、向南走3m C、向西走3m D、向北走3m2. 下列各图中,能正确表示数轴的是( )A、
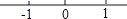 B、
B、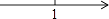 C、
C、 D、
D、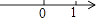 3. 数轴上点A表示﹣4,点B表示2,则表示A,B两点间的距离的算式是)A、﹣4+2 B、﹣4﹣2 C、2﹣(﹣4) D、2﹣44. 下表是我国几个城市某年一月份的平均气温,其中气温最低的城市是( )
3. 数轴上点A表示﹣4,点B表示2,则表示A,B两点间的距离的算式是)A、﹣4+2 B、﹣4﹣2 C、2﹣(﹣4) D、2﹣44. 下表是我国几个城市某年一月份的平均气温,其中气温最低的城市是( )城市
北京
武汉
广州
哈尔滨
平均气温
(单位℃)
﹣4.6
3.8
13.1
﹣19.4
A、北京 B、武汉 C、广州 D、哈尔滨5. 下列说法正确的是( )①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的表面是长方形.
A、①② B、①③ C、②③ D、①②③6. 下列说法正确的是( )A、射线AB与射线BA表示同一条射线 B、连接两点的线段叫做这两点的距离 C、平角是一条直线 D、若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠37. 苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )A、(a+b)元 B、(3a+2b)元 C、(2a+3b)元 D、5(a+b)元8. 下列说法正确的是( )
A、0不是单项式 B、x没有系数 C、是多项式 D、﹣xy5是单项式9. 若关于x的方程mxm﹣2﹣m+3=0是一元一次方程,则这个方程的解是( )A、x=0 B、x=3 C、x=﹣3 D、x=210. 某商人在一次买卖中均以120元卖出两件衣服,一件赚25%,一件赔25%,在这次交易中,该商人( )A、赚16元 B、赔16元 C、不赚不赔 D、无法确定二、填空题
-
11. 小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数共有个.
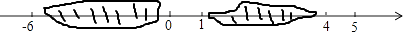 12. 已知∠α=53°27′,则它的余角等于 .13. 当x=1时,代数式4﹣3x的值是 .14. 已知单项式3amb2与﹣ a4bn﹣1是同类项,那么4m﹣n= .15. 一个多项式与﹣x2﹣2x+11的和是3x﹣2,则这个多项式为 .16. 已知|x|=3,|y|=4,且x>y,则2x﹣y的值为 .17. 若时钟由2点30分走到2点55分,则时针、分针转过的角度分别为 .18. 如图,已知点O是直线AD上的点,∠AOB、∠BOC、∠COD三个角从小到大依次相差25°,则这三个角的度数分别为 .
12. 已知∠α=53°27′,则它的余角等于 .13. 当x=1时,代数式4﹣3x的值是 .14. 已知单项式3amb2与﹣ a4bn﹣1是同类项,那么4m﹣n= .15. 一个多项式与﹣x2﹣2x+11的和是3x﹣2,则这个多项式为 .16. 已知|x|=3,|y|=4,且x>y,则2x﹣y的值为 .17. 若时钟由2点30分走到2点55分,则时针、分针转过的角度分别为 .18. 如图,已知点O是直线AD上的点,∠AOB、∠BOC、∠COD三个角从小到大依次相差25°,则这三个角的度数分别为 . 19. 已知方程 的解也是方程|3x﹣2|=b的解,则b= .20. 小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是:2y﹣ = y﹣▌,怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=﹣ ,于是很快补好了这个常数,你能补出这个常数是多少吗?它应是 .
19. 已知方程 的解也是方程|3x﹣2|=b的解,则b= .20. 小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是:2y﹣ = y﹣▌,怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=﹣ ,于是很快补好了这个常数,你能补出这个常数是多少吗?它应是 .三、解答题
-
21. 计算:
(1)、 ﹣|﹣1 |﹣(+2 )﹣(﹣2.75)(2)、﹣14﹣[1﹣(1﹣0.5× )]×6.22. 一只小虫从某点P出发,在一条直线上来回爬行,假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:厘米)依次为:+5,﹣3,+10,﹣8,﹣6,+12,﹣10.(1)、通过计算说明小虫是否回到起点P.(2)、如果小虫爬行的速度为0.5厘米/秒,那么小虫共爬行了多长时间.23. 如图所示,已知∠AOC=∠BOD=100°,且∠AOB:∠AOD=2:7,求∠BOC和∠COD的度数.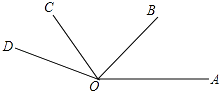 24. 请根据图中提供的信息,回答下列问题:
24. 请根据图中提供的信息,回答下列问题: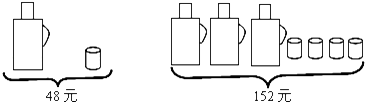 (1)、一个水瓶与一个水杯分别是多少元?(2)、甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)25. 已知A=x2﹣2x+1,B=2x2﹣6x+3.
(1)、一个水瓶与一个水杯分别是多少元?(2)、甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)25. 已知A=x2﹣2x+1,B=2x2﹣6x+3.求:
(1)、A+2B.(2)、2A﹣B.26. 观察下列解题过程:计算:1+5+52+53+…+524+525的值.
解:设S=1+5+52+53+…+524+525 , ⑴
则5S=5+52+53+…+525+526⑵
⑵﹣⑴,得4S=526﹣1
S=
通过阅读,你一定学会了一种解决问题的方法,请用你学到的方法计算:
(1)、1+3+32+33+…+39+310(2)、1+x+x2+x3+…+x99+x100 .27. 观察图,解答下列问题.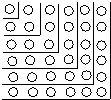 (1)、图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?(2)、某一层上有65个圆圈,这是第几层?
(1)、图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?(2)、某一层上有65个圆圈,这是第几层?
(3)、数图中的圆圈个数可以有多种不同的方法.比如:前两层的圆圈个数和为(1+3)或22 ,
由此得,1+3=22 .
同样,
由前三层的圆圈个数和得:1+3+5=32 .
由前四层的圆圈个数和得:1+3+5+7=42 .
由前五层的圆圈个数和得:1+3+5+7+9=52 .
…
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)、计算:1+3+5+…+99的和;(5)、计算:101+103+105+…+199的和.