2017-2018学年人教版数学八年级下册同步训练：18.1.1《平行四边形的性质》
试卷更新日期：2018-02-09 类型：同步测试
一、选择题
-
1. 平行四边形的两邻角的角平分线相交所成的角为（ ）．A、锐角 B、直角 C、钝角 D、不能确定2. 平行四边形的周长为24，相邻两边的差为2，则平行四边形的各边长为（ ）．A、4，4，8，8 B、5，5，7，7 C、5.5，5.5，6.5，6.5 D、3，3，9，93. 如图所示，四边形ABCD是平行四边形，∠D＝120°，∠CAD＝32°，则∠ABC、∠CAB的度数分别为（ ）．
A、28°，120° B、120°，28° C、32°，120° D、120°，32°4. 在平行四边形ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（ ）．A、1∶2∶3∶4 B、1∶2∶2∶1 C、1∶1∶2∶2 D、2∶1∶2∶15. 下面的性质中，平行四边形不一定具有的是（ ）．A、对角互补 B、邻角互补 C、对角相等 D、对边相等.6. 在平行四边形ABCD中，∠A的平分线交DC于E，若∠DEA＝30°，则∠B＝（ ）．A、100° B、120° C、135° D、150°7. 如图，平行四边形ABCD中，EF过对角线的交点O，AB＝4，AD＝3，OF＝1.3，则四边形BCEF的周长为（ ）
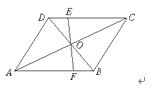A、8.3 B、9.6 C、12.6 D、13.68. 如图，在平行四边形ABCD中，下列各式不一定正确的是（ ）．
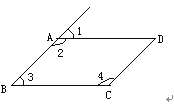A、 B、 C、 D、9. 平行四边形的周长为25 ，对边的距离分别为2 、3 ，则这个平行四边形的面积为（ ）
A、15 2 B、25 2 C、30 2 D、50 210. 已知O为平行四边形ABCD对角线的交点，△AOB的面积为1，则平行四边形的面积为（ ）A、1 B、2 C、3 D、411. 平行四边形的对角线分别为 ，一边长为12，则 的值可能是下列各组数中的（ ）A、8与14 B、10与14 C、18与20 D、10与2812. 平行四边形ABCD中，如果∠B=100°，那么∠A、∠D的值分别是（ ）A、∠A=80°，∠D=100° B、∠A=100°，∠D=80° C、∠B=80°，∠D=80° D、∠A=100°，∠D=100°13. 若平行四边形ABCD的周长为28，△ABC的周长为17cm，则AC的长为 （ ）A、11cm B、5.5cm C、4cm D、3cm14. 在给定的条件中，能作出平行四边形的是（ ）A、以60cm为对角线，20cm、34cm为两条邻边 B、以20cm、36cm为对角线，22cm为一条边 C、以6cm为一条对角线，3cm、10cm为两条邻边 D、以6cm、10cm为对角线，8cm为一条边15. 四边形ABCD，仅从下列条件中任取两个加以组合，使得ABCD是平行四边形，一共有多少种不同的组合？ AB∥CD BC∥AD AB=CD BC=AD（ ）A、2组 B、3组 C、4组 D、6组二、填空题
-
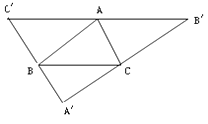
16. 如图所示，A′B′∥AB，B′C′∥BC，C′A′∥CA，图中有个平行四边形．
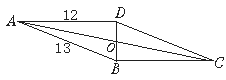
17. 已知：平行四边形一边AB＝12 cm，它的长是周长的 ，则BC＝cm，CD＝ cm.
18. 平行四边形的一组对角度数之和为200°，则平行四边形中较大的角为.19. 平行四边形ABCD中，若∠A∶∠B＝1∶3，那么∠A＝ ， ∠B＝ ， ∠C＝ ， ∠D＝.20. 如图所示，在平行四边形ABCD中，对角线AC、BD相交于点O，图中全等三角形共有对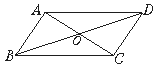
三、解答题
-
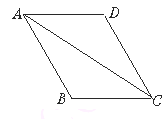
21. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，MN是过O点的直线，交BC于M，交AD于N，BM＝2，AN＝2.8，求BC和AD的长.
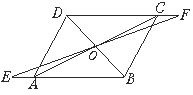
22. 如图所示，已知平行四边形ABCD的对角线交于O，过O作直线交AB、CD的反向延长线于E、F，求证：OE＝OF.
