2017-2018学年人教版数学八年级下册同步训练： 17.2《勾股定理的逆定理》

试卷更新日期：2018-02-09 类型：同步测试

进入出卷网下载

一、单选题

1. 若△ABC三边长a，b，c满足 $\sqrt{a + b - 25}$ +| $b - a - 1$ |+（ $c - 5$ ）²=0，则△ABC是（）

A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
2. 在平面直角坐标系中，点A的坐标为（1，1），点B的坐标为（11，1），点C到直线AB的距离为5，且△ABC是直角三角形，则满足条件的C点有（　　）

A、4个 B、5个 C、6个 D、8个

查看试题解析
3. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（）

A、90° B、60° C、45° D、30°

查看试题解析
4. 长度为9、12、15、36、39的五根木棍，从中取三根依次搭成三角形，最多可搭成直角三角形的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
5. 如图所示，在由单位正方形组成的网格图中标有AB，CD，EF，GH四条线段，其中能构成直角三角形三边的线段是(　　)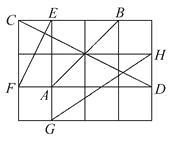

A、CD，EF，GH B、AB，EF，GH C、AB，CD，GH D、AB，CD，EF

查看试题解析
6. 如图所示方格纸中的三角形是（　　）

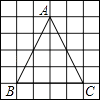A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
7. 将直角三角形三条边的长度都扩大同样的倍数后得到的三角形(　　)

A、仍是直角三角形 B、可能是锐角三角形 C、可能是钝角三角形 D、不可能是直角三角形

查看试题解析
8. 满足下列条件的三角形中，不是直角三角形的是（　　）

A、三内角之比为1：2：3 B、三边长的平方之比为1：2：3 C、三边长之比为3：4：5 D、三内角之比为3：4：5

查看试题解析
9. 下列说法正确的有（　　）
①如果∠A+∠B=∠C，那么△ABC是直角三角形；②如果∠A：∠B：∠C=1：2：3，则三角形是直角三角形；③如果三角形的三边长分别为4、4、6，那么这个三角形不是直角三角形；④有一个角是直角的三角形是直角三角形．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 有四个三角形，分别满足下列条件：（1）一个角等于另外两个内角之和；（2）三个内角之比为3：4：5；（3）三边之比为5：12：13；（4）三边长分别为5，24，25．其中直角三角形有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. △ABC中，∠A、∠B、∠C的对边分别是a、b、c，下列说法中，错误的是（　　）

A、如果∠C﹣∠B=∠A，那么∠C=90° B、如果∠C=90°，那么c²﹣b²=a² C、如果（a+b）（a﹣b）=c² ，那么∠C=90° D、如果∠A=30°∠B=60°，那么AB=2BC

查看试题解析
12. 下列说法中，正确的个数有（）
①已知直角三角形的面积为2，两直角边的比为1：2，则斜边长为 $\sqrt{10}$ ；
②直角三角形的最大边长为 $\sqrt{3}$ ，最短边长为1，则另一边长为 $\sqrt{2}$ ；
③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；
④等腰三角形面积为12，底边上的高为4，则腰长为5．

A、1个 B、2个 C、3个 D、4个

查看试题解析
13. 下列说法：①已知直角三角形的面积为4，两直角边的比为1：2，则斜边长为 $\sqrt{10}$ ；②直角三角形的最大边长为 $\sqrt{3}$ ，最短边长为1，则另一边长为 $\sqrt{2}$ ；③在△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC为直角三角形；④等腰三角形面积为12，底边上的高为4，则腰长为5，其中正确结论的序号是（）

A、只有①②③ B、只有①②④ C、只有③④ D、只有②③④

查看试题解析
14. 下列结论中，错误的有（　　）
①Rt△ABC中，已知两边分别为3和4，则第三边的长为5；

②三角形的三边分别为a、b、c ，若a²+b²=c² ，则∠A=90°；

③若△ABC中，∠A：∠B：∠C=1：5：6，则这个三角形是一个直角三角形；

④若（x﹣y）²+M=（x+y）²成立，则M=4xy ．

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

15. 观察以下几组勾股数，并寻找规律：
①3，4，5；
②5，12，13；
③7，24，25；
④9，40，41，…
请你写出有以上规律的第⑤组勾股数：

查看试题解析
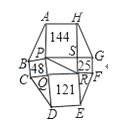
16.
如图，已知八边形ABCDEFGH中4个正方形的面积分别为25，144，48，121个平方单位，PR=13（单位），则该八边形的面积=平方单位．

查看试题解析
17. 若a，b，c是直角三角形的三条边长，斜边c上的高的长是h，给出下列结论：
①以a² ， b² ， c²的长为边的三条线段能组成一个三角形；②以 $\sqrt{a}$ ， $\sqrt{b}$ ， $\sqrt{c}$ 的长为边的三条线段能组成一个三角形；③以a+b，c+h，h的长为边的三条线段能组成直角三角形；④以 $\frac{1}{a}$ ， $\frac{1}{b}$ ， $\frac{1}{c}$ 的长为边的三条线段能组成直角三角形，正确结论的序号为．

查看试题解析
18. 已知|m﹣ $\sqrt{2}$ |+ $\sqrt{n - 2}$ +（p﹣ $\sqrt{2}$ ）²=0则以m、n、p为三边长的三角形是三角形．

查看试题解析
19. 已知x，y，z均为正数，且|x﹣4|+（y﹣3）2+ $\sqrt{y + z - 8}$ =0，若以x，y，z的长为边长画三角形，此三角形的形状为．

查看试题解析

三、解答题

20.
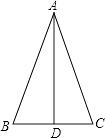
一如图，在△ABC中，AB=41cm，BC=18cm，BC边上的中线AD=40cm．△ABC是等腰三角形吗？为什么？

查看试题解析
21. 当a、b、c为何值时，代数式 $\sqrt{a - 3} + b^{2} + c^{2} - 10 b - 8 c + 6_{}$ 有最小值？并求出这个最小值和此时以a、b、c值为边的三角形的面积．

查看试题解析
22. 已知a，b，c为正数，满足如下两个条件：
a+b+c=32 ①
$\frac{b + c - a}{b c} + \frac{c + a - b}{c a} + \frac{a + b - c}{a b} = \frac{1}{4}$ ②
是否存在以 $\sqrt{a}$ ， $\sqrt{b}$ ， $\sqrt{c}$ 为三边长的三角形？如果存在，求出三角形的最大内角．

查看试题解析
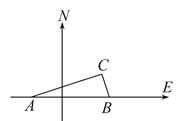
23.
如图，在我国沿海有一艘不明国籍的轮船进入我国海域，我海军甲、乙两艘巡逻艇立即从相距13nmile的A，B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120nmile，乙巡逻艇每小时航行50nmile，航向为北偏西40°，问：甲巡逻艇的航向是多少？

查看试题解析
24. 综合题

(1)、如图①所示，P是等边△ABC内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转60°得△BCQ，连接PQ．若PA2+PB2=PC2，证明∠PQC=90°；

(2)、如图②所示，P是等腰直角△ABC（∠ABC=90°）内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转90°得△BCQ，连接PQ．当PA、PB、PC满足什么条件时，∠PQC=90°？请说明．

查看试题解析