2017-2018学年人教版数学八年级下册同步训练： 17.1《勾股定理》
试卷更新日期：2018-02-09 类型：同步测试
一、单选题
-
1. 如图，小方格都是边长为1的正方形，则四边形ABCD的面积是（ ）
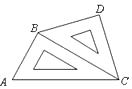
A、25 B、12.5 C、9 D、8.52.如图，AB⊥CD于B，△ABD和△BCE都是等腰直角三角形，如果CD=17，BE=5，那么AC的长为（ ）
A、12 B、7 C、5 D、133. 如图，在△ABC中，AD⊥BC于D，AB=3，BD=2，DC=1，则AC=（ ）
A、6 B、 C、 D、44. 已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（ ）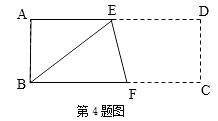
A、6cm2 B、8cm2 C、10cm2 D、12cm25. 如下图五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ）A、
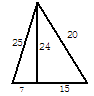B、
C、
D、
6. 一直角三角形的三边分别为2、3、x，那么以x为边长的正方形的面积为（ ）
A、13 B、5 C、13或5 D、无法确定7. 等腰三角形的腰长为10，底长为12，则其底边上的高为( )A、13 B、8 C、25 D、648. 已知一个Rt△的两边长分别为3和4，则第三边长的平方是（ ）A、25 B、14， C、7 D、7或259. 直角三角形的斜边比一直角边长2 cm，另一直角边长为6 cm，则它的斜边长( ).A、4 cm B、8 cm C、10 cm D、12 cm10. 如图，已知矩形A′BOC的边长A′B=2，OB=1，数轴上点A表示的数为x，则x2﹣13的立方根是（ ）
A、 ﹣13 B、﹣ ﹣13 C、2 D、﹣211. 如图，正方形OABC的边长为1，以A为圆心，AC为半径画弧，与数轴的一个交点是D，则D点表示的数为（ ）
A、1- B、 -1 C、 D、12. 已知等边△ABC，点A在坐标原点，B点的坐标为（6，0），则点C的坐标为（ ）
A、（3，3） B、（3，2 ） C、（2 ，3） D、（3，3 ）13. 如图是我校的长方形水泥操场，如果一学生要A角走到C角，至少走（ ）
A、140米 B、120米 C、100米 D、90米14. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的边长分别是3，5，2，3，则最大正方形E的面积是（ ）
A、13 B、26 C、47 D、9415. 如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（ ）
A、5 B、25 C、10 +5 D、35二、填空题
-
16. 某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要米17. 在直角三角形
中，斜边 =2，则 
= 18. 飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行千米19. 在边长为1cm的正△ABC中，P0为BC边上一点，作P0P1⊥CA于点 P1 ， 作P1P2⊥AB于点P2 ， 作P2P3⊥BC于点P3 ． 如果点P3恰与点P0重合，则△P1P2P3的面积是cm2 ．20. 如图，正方形BCDE和ABFG的边长分别为2a，a，连接CE和CG，则图中阴影部分的面积是 ；CE和CG的大小关系 ．
三、解答题
，求 的长．
. 