安徽省合肥市瑶海区2015-2016学年七年级上学期数学期末考试试卷
试卷更新日期：2018-02-09 类型：期末考试
一、单选题
-
1. ﹣3的绝对值是（ ）A、3 B、﹣3 C、 D、-2. 在﹣2，0，2，﹣3这四个数中，最小的数是（ ）A、2 B、0 C、﹣2 D、﹣33. 2015年3月29日，习近平主席同出席博鳌亚洲论坛年会的中外企业家代表座谈时说：通过“一带一路”，我们希望用10年左右的时间，使中国同沿线国家的年贸易额突破2.5万亿美元.2.5万亿用科学记数法表示为（ ）A、2.5×104 B、2.5×108 C、2.5×1012 D、25×10114. 下列运算中结果正确的是（ ）A、3a+2b=5ab B、5y﹣3y=2 C、﹣3x+5x=﹣8x D、3x2y﹣2x2y=x2y5. 在下列调查中，适宜采用全面调查的是（ ）A、了解我省中学生的视力情况 B、了解七(1)班学生校服的尺码情况 C、检测一批电灯泡的使用寿命 D、调查安徽卫视《超级演说家》栏目的收视率6. 有理数a、b在数轴上的位置如图所示，下列各式成立的是（ ）
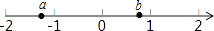A、a+b＞0 B、a﹣b＞0 C、ab＞0 D、 ＜07. 已知a，b满足方程组 ，则a+b的值为（ ）A、﹣4 B、4 C、﹣2 D、28. 如图，C、D是线段AB上两点，若CD=4cm，DB=7cm，且B是AC的中点，则AC的长等于（ ）
A、3cm B、6cm C、11cm D、14cm9.如图，将4×3的网格图剪去5个小正方形后，图中还剩下7个小正方形，为了使余下的部分（小正方形之间至少要有一条边相连）恰好能折成一个正方体，需要再剪去1个小正方形，则应剪去的小正方形的编号是（ ）
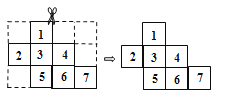A、7 B、6 C、5 D、410. 找出以下图形变化的规律，则第2016个图形中黑色正方形的数量是（ ）
A、3021 B、3022 C、3023 D、302411. 如果∠α和∠β互补，且∠α＞∠β，则下列表示角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．能表示∠β的余角的是 . （填写序号）
二、填空题
-
12. 2的相反数是 ．13. 试写出一个解为x=1的一元一次方程： ．14. 某学校“你最喜爱的球类运动”调查中，随机调查了若干名学生（每个学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为名．
三、解答题
-
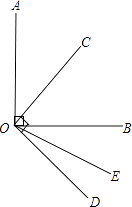
15. 计算：﹣12+3×（﹣2）3﹣（﹣6）÷（﹣ ）2 ．16. 解方程：2﹣ = ．17. 如图，∠AOB=∠COD=90°，OC平分∠AOB，∠BOD=3∠DOE．试求∠COE的度数．
18. 解方程组 ．19. 老师在黑板上书写了一个正确的演算过程，随后用一张纸挡住了一个二次三项式，形式如下：
﹣3x=x2﹣5x+1 (1)、求所挡的二次三项式；(2)、若x=﹣1，求所挡的二次三项式的值．
20. 已知一道路沿途5个车站A、B、C、D、E，它们之间的距离如图所示（km）
(1)、求D、E两站之间的距离；(2)、如果a=8，D为线段AE的中点，求b的值．21. 为了深化改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团．为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表（不完整）：某校被调查学生选择社团意向统计表
选择意向
所占百分比
文学鉴赏
a
科学实验
35%
音乐舞蹈
b
手工编织
10%
其他
c
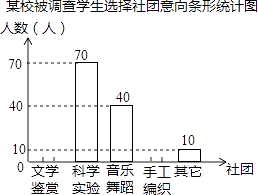
根据统计图表中的信息，解答下列问题：
(1)、求本次调查的学生总人数及a，b，c的值；
(2)、将条形统计图补充完整；
(3)、若该校共有1200名学生，试估计全校选择“科学实验”社团的人数．22. 为实现教育均衡发展，打造新优质学校，瑶海区计划对A、B两类薄弱学校全部进行改造，根据预算，共需资金1575万元．改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元，求改造一所A类学校和一所B类学校所需的资金分别是多少万元？23. 观察图形，解答问题：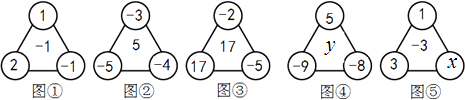
(1)、按下表已填写的形式填写表中的空格：图①
图②
图③
三个角上三个数的积
1×（﹣1）×2=﹣2
（﹣3）×（﹣4）×（﹣5）=﹣60
三个角上三个数的和
1+（﹣1）+2=2
（﹣3）+（﹣4）+（﹣5）=﹣12
积与和的商
﹣2÷2=﹣1
(2)、请用你发现的规律求出图④中的数y和图⑤中的数x．