2015-2016学年广东省潮州市饶平县八年级下学期期末数学试卷
试卷更新日期：2016-11-09 类型：期末考试
一、选择题
-
1. 计算 的结果是（ ）A、1 B、﹣1 C、±1 D、﹣22. 下列二次根式中，能与 合并的是（ ）A、 B、 C、 D、3. 下列说法正确的是（ ）A、已知a、b、c是三角形的三边长，则a2+b2=c2 B、在直角三角形中，两边的平方和等于第三边的平方 C、在Rt△ABC中，∠C=90°，a、b、c分别是∠A，∠B，∠C的对边，则a2+b2=c2 D、在Rt△ABC中，∠B=90°，a、b、c分别是∠A，∠B，∠C的对边，则a2+b2=c24. 已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）A、当∠ABC=90°时，它是矩形 B、当AC=BD时，它是正方形 C、当AB=BC时，它是菱形 D、当AC⊥BD时，它是菱形5. 矩形的面积是48cm2 ， 一边与一条对角线的比是4：5，则该矩形的对角线长是（ ）A、6cm B、8cm C、10cm D、24cm6. 一个长方形的面积是10cm2 ， 其长是acm，宽是bcm，下列判断错误的是（ ）A、10是常量 B、10是变量 C、b是变量 D、a是变量7. 一次函数y=﹣x+1的图象不经过的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 某同学使用计算器求15个数的平均数时，错将其中一个数据15输入为45，那么由此求得的平均数与实际平均数的差是（ ）A、2 B、3 C、﹣2 D、﹣3
二、填空题
-
9. 计算： • = ．10. 若一个三角形三边的长度之比为3：4：5，且周长为60cm，则它的面积是 cm2 ．11. 如图，菱形ABCD中，∠A=60°，BD=3，则菱形ABCD的周长是 ．
12. 若点A（1，y1）和点B（2，y2）都在一次函数y=﹣x+2的图象上，则y1y2（选择“＞”、“＜”、=”填空）．13. 中学生田径运动会上，参加男子跳高的15名运动员的成绩如表：跳高成绩（m）
1.50
1.55
1.60
1.65
1.70
1.75
人数
1
3
3
3
4
1
这些运动员跳高成绩的众数是 ．
14. 一组数据的方差s2= [（x1﹣3）2+（x2﹣3）2+…+（x20﹣3）2]，则这组数据的平均数是 ．三、解答题
-
15. 计算：（ + ）（ ﹣1）16. 如图，台风过后，一所学校的旗杆在离地某处断裂，旗杆顶部落在离旗杆底部12米处，已知旗杆原长24米，求旗杆在离底部多少米的位置断裂？
17. 已知：在平面直角坐标系xOy中，一次函数y=kx+2的图象与y轴交于点A，与x轴的正半轴交于点B，OA=2OB．(1)、直接写出点A、点B的坐标；(2)、在所给平面直角坐标系内画一次函数的图象．
18. 如果三角形的三边长a，b，c满足 +|12﹣b|+（a﹣13）2=0，你能确定这个三角形的形状吗？请说明理由．19. 小丽上午9：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中，小丽离家的距离y（米）和所经过的时间x（分）之间的函数关系图象如图所示．请根据图象回答下列问题：
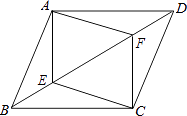
(1)、小丽去超市途中的速度是米/分；在超市逗留了分；(2)、求小丽从超市返回家中所需要的时间？20. 已知：如图，在▱ABCD中，E、F是对角线BD上的两点，且BE=DF，求证：四边形AECF是平行四边形．
四、解答题
-
21. 某校八年级（1）班组织了一次朗读比赛，A队10人的比赛成绩（10分制）分别是：10、8、7、9、8、10、10、9、10、9．(1)、计算A队的平均成绩和方差；(2)、已知B队成绩的方差是1.4，问哪一队成绩较为整齐？
