2015-2016学年北京市西城区八年级下学期期末数学试卷

试卷更新日期：2016-11-09 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 下列二次根式中，是最简二次根式的是（  ）
    A、15 B、12 C、13 D、9

    查看试题解析

  • 2. 平行四边形ABCD中，若∠B=2∠A，则∠C的度数为（  ）

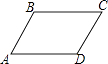    A、120° B、60° C、30° D、15°

    查看试题解析

  • 3. 甲、乙、丙、丁四人进行射击测试，每人测试10次，平均成绩均为9.2环，方差如表所示

     选手

     甲

     乙

     丙

     丁

     方差

     0.56

     0.60

     0.50

     0.45

    则在这四个选手中，成绩最稳定的是（  ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 4. 若A（1，y1），B（2，y2）两点都在反比例函数y= 1x 的图象上，则y1与y2的大小关系是（  ）
    A、y1＜y2 B、y1=y2 C、y1＞y2 D、无法确定

    查看试题解析

  • 5. 如图，菱形ABCD的两条对角线AC，BD相交于点O，若AC=4，BD=6，则菱形ABCD的周长为（  ）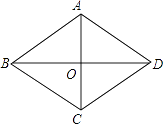

    A、16 B、24 C、4 13 D、8 13

    查看试题解析

  • 6. 下列命题中，正确的是（  ）
    A、有一组邻边相等的四边形是菱形 B、对角线互相平分且垂直的四边形是矩形 C、两组邻角相等的四边形是平行四边形 D、对角线互相垂直且相等的平行四边形是正方形

    查看试题解析

  • 7. 如图，正方形ABCD的两条对角线AC，BD相交于点O，点E在BD上，且BE=CD，则∠BEC的度数为（  ）

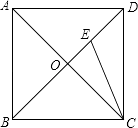    A、22.5° B、60° C、67.5° D、75°

    查看试题解析

  • 8. 关于x的一元二次方程x2﹣2x+k=0有两个实数根，则实数k的取值范围是（  ）
    A、k≤1 B、k＞1 C、k=1 D、k≥1

    查看试题解析

  • 9. 已知正比例函数y=kx的图象与反比例函数y= mx 的图象交于A，B两点，若点A的坐标为（﹣2，1），则关于x的方程 mx =kx的两个实数根分别为（  ）
    A、x1=﹣1，x2=1 B、x1=﹣1，x2=2 C、x1=﹣2，x2=1 D、x1=﹣2，x2=2

    查看试题解析

  • 10. 中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽，他为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是用八个全等的直角三角形拼接而成．将图中正方形MNKT，正方形EFGH，正方形ABCD的面积分别记为S1 ， S2 ， S3 ， 若S1+S2+S3=18，则正方形EFGH的面积为（  ）

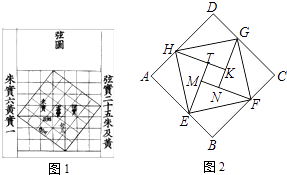    A、9 B、6 C、5 D、92

    查看试题解析

二、填空题

  • 11. 关于x的一元二次方程x2﹣6x+m=0有一个根为2，则m的值为 ．

    查看试题解析

  • 12. 如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为 ．

    查看试题解析

  • 13. 某校开展了“书香校园”的活动，小腾班长统计了本学期全班40名同学课外图书的阅读数量（单位：本），绘制了折线统计图（如图所示），在这40名学生的图书阅读数量中，中位数是 ．

    查看试题解析

  • 14. 将一元二次方程x2+4x+1=0化成（x+a）2=b的形式，其中a，b是常数，则a+b=

    查看试题解析

  • 15. 反比例函数y= kx 在第一象限的图象如图，请写出一个满足条件的k值，k=

    查看试题解析

  • 16. 如图，将矩形ABCD沿对角线BD所在直线折叠，点C落在同一平面内，落点记为C′，BC′与AD交于点E，若AB=3，BC=4，则DE的长为 ．

    查看试题解析

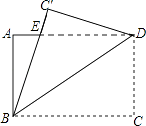  • 17. 如图，平安路与幸福路是两条平行的道路，且与新兴大街垂直，老街与小米胡同垂直，书店位于老街与小米胡同的交口处，如果小强同学站在平安路与新兴大街的交叉路口，准备去书店，按图中的街道行走，最近的路程为 m．

    查看试题解析

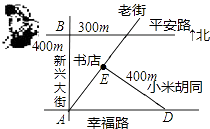  • 18.

    如图，在△ABC中，点P从点A出发向点C运动，在运动过程中，设x表示线段AP的长，y表示线段BP的长，y与x之间的关系如图2所示，则线段AB的长为 ， 线段BC的长为 ．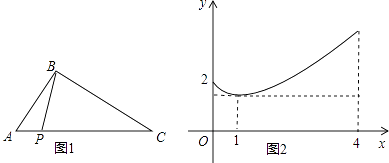

    查看试题解析

三、解答题

四、解答题

  • 21. 如图，在▱ABCD中，点E，M分别在边AB，CD上，且AE=CM，点F，N分别在边BC，AD上，且DN=BF．

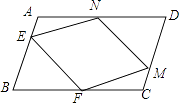    (1)、求证：△AEN≌△CMF；
    (2)、连接EM，FN，若EM⊥FN，求证：EFMN是菱形．

    查看试题解析

  • 22. 为了让同学们了解自己的体育水平，初二1班的体育康老师对全班45名学生进行了一次体育模拟测试（得分均为整数）成绩满分为10分，成绩达到9分以上（包含9分）为优秀，成绩达到6分以上（包含6分）为合格，1班的体育委员根据这次测试成绩，制作了统计图和分析表如下：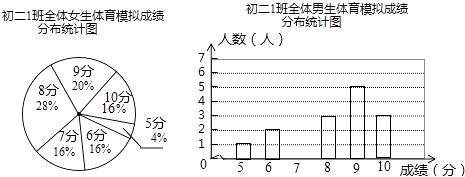

    初二1班体育模拟测试成绩分析表

     平均分

     方差

     中位数

     众数

     合格率

     优秀率

     男生

     2

     8

     7

     95%

     40%

     女生

     7.92

     1.99

     8

     96%

     36%

    根据以上信息，解答下列问题：

    (1)、在这次测试中，该班女生得10分的人数为4人，则这个班共有女生人；
    (2)、补全初二1班男生体育模拟测试成绩统计图，并把相应的数据标注在统计图上；
    (3)、补全初二1班体育模拟测试成绩分析表；
    (4)、你认为在这次体育测试中，1班的男生队、女生队哪个表现更突出一些？并写出一条支持你的看法的理由；
    (5)、体育康老师说，从整体看，1班的体育成绩在合格率方面基本达标，但在优秀率方面还不够理想，因此他希望全班同学继续加强体育锻炼，争取在期末考试中，全班的优秀率达到60%，若男生优秀人数再增加6人，则女生优秀人数再增加多少人才能完成康老师提出的目标？

    查看试题解析

  • 23. 已知：如图，在四边形ABCD中，∠B=90°，AB=BC=2，CD=3，AD=1，求∠DAB的度数．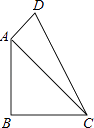

    查看试题解析

  • 24. 如图，矩形ABCD的对角线AC，BD相交于点O，点E，F，M，N分别为OA，OB，OC，OD的中点，连接EF，FM，MN，NE．

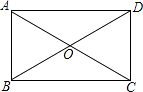    (1)、依题意，补全图形；
    (2)、求证：四边形EFMN是矩形；
    (3)、连接DM，若DM⊥AC于点M，ON=3，求矩形ABCD的面积．

    查看试题解析

  • 25. 在平面直角坐标系xOy中，四边形OABC是矩形，点B的坐标为（4，3），反比例函数y= mx 的图象经过点B．

    (1)、求反比例函数的解析式；
    (2)、一次函数y=ax﹣1的图象与y轴交于点D，与反比例函数y= mx 的图象交于点E，且△ADE的面积等于6，求一次函数的解析式；
    (3)、在（2）的条件下，直线OE与双曲线y= kx （x＞0）交于第一象限的点P，将直线OE向右平移 214 个单位后，与双曲线y= kx （x＞0）交于点Q，与x轴交于点H，若QH= 12 OP，求k的值．

    查看试题解析

五、填空题

  • 26. 如图，在数轴上点A表示的实数是 ．

    查看试题解析

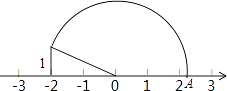  • 27. 我们已经学习了反比例函数，在生活中，两个变量间具有反比例函数关系的实例有许多，例如：在路程s一定时，平均速度v是运行时间t的反比例函数，其函数关系式可以写为：v= st （s为常数，s≠0）．

    请你仿照上例，再举一个在日常生活、学习中，两个变量间具有反比例函数关系的实例：；并写出这两个变量之间的函数解析式： ．

    查看试题解析

六、解答题

  • 28. 已知：关于x的一元二次方程mx2﹣3（m﹣1）x+2m﹣3=0（m＞3）．
    (1)、求证：方程总有两个不相等的实数根；
    (2)、设方程的两个实数根分别为x1 ， x2（用含m的代数式表示）；

    ①求方程的两个实数根x1 ， x2（用含m的代数式表示）；

    ②若mx1＜8﹣4x2 ， 直接写出m的取值范围．

    查看试题解析

  • 29. 四边形ABCD是正方形，对角线AC，BD相交于点O．

    (1)、

    如图1，点P是正方形ABCD外一点，连接OP，以OP为一边，作正方形OPMN，且边ON与边BC相交，连接AP，BN．

    ①依题意补全图1；

    ②判断AP与BN的数量关系及位置关系，写出结论并加以证明；

    (2)、点P在AB延长线上，且∠APO=30°，连接OP，以OP为一边，作正方形OPMN，且边ON与BC的延长线恰交于点N，连接CM，若AB=2，求CM的长（不必写出计算结果，简述求CM长的过程）

    查看试题解析