2015-2016学年安徽省亳州市谯城区八年级上学期期末数学试卷
试卷更新日期:2016-11-09 类型:期末考试
一、选择题
-
1. 点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )A、(1,﹣8) B、(1,﹣2) C、(﹣6,﹣1) D、(0,﹣1)2. 若三角形的三边长分别为3,4,x , 则x的值可能是( )A、1 B、6 C、7 D、103. 一个三角形的三个外角之比为3:4:5,则这个三角形内角之比是( )A、5:4:3 B、4:3:2 C、3:2:1 D、5:3:14. 下列函数中,y是x的一次函数的是( )
①y=x﹣6;②y=;③y=;④y=7﹣x.
A、①②③ B、①③④ C、①②③④ D、②③④5. 若直线y=mx+2m﹣3经过二、三、四象限,则m的取值范围是( )A、m< B、m>0 C、m> D、m<06. 下列四个图形中,线段BE是△ABC的高的是( )A、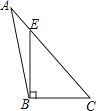 B、
B、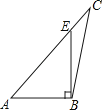 C、
C、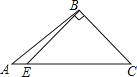 D、
D、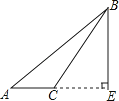 7. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
7. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )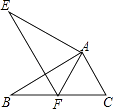 A、1个 B、2个 C、3个 D、4个8. 小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地,下列函数图象能表达这一过程的是( )A、
A、1个 B、2个 C、3个 D、4个8. 小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地,下列函数图象能表达这一过程的是( )A、 B、
B、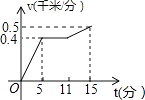 C、
C、 D、
D、 9. 如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠C的度数是( )
9. 如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠C的度数是( ) A、30° B、45° C、55° D、60°10.
A、30° B、45° C、55° D、60°10.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
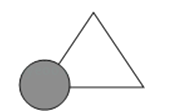 A、SSS B、SAS C、AAS D、ASA
A、SSS B、SAS C、AAS D、ASA二、填空题
-
11. 函数y= 中,自变量x的取值范围是 .12. 直线y=kx+b与直线y=﹣2x+1平行,且经过点(﹣2,3),则kb= .13.
如图,一次函数y=x+6的图象经过点P(a,b)和Q(c,d),则a(c﹣d)﹣b(c﹣d)的值为 .
 14. y+2与x+1成正比例,且当x=1时,y=4,则当x=2时,y= .15. 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2 , 则△BEF的面积: cm2 .
14. y+2与x+1成正比例,且当x=1时,y=4,则当x=2时,y= .15. 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为16cm2 , 则△BEF的面积: cm2 . 16. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
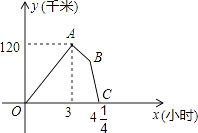
16. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3 ,75);
④快递车从乙地返回时的速度为90千米/时,
以上4个结论正确的是 .
三、解答题
-
17. 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
 (1)、写出点A、B的坐标:
(1)、写出点A、B的坐标:A( , )、B( , )
(2)、将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).(3)、△ABC的面积为 .18. 已知直线y=kx+b经过点A(5,0),B(1,4).(1)、求直线AB的解析式;(2)、若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式2x﹣4>kx+b的解集. 19. 如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.
19. 如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数. 20. 某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
20. 某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:类型 价格
进价(元/盏)
售价(元/盏)
A型
30
45
B型
50
70
(1)、设商场购进A型节能台灯为x盏,销售完这批台灯时可获利为y元,求y关于x的函数解析式;(2)、若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?21. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.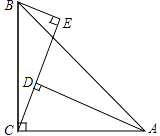 (1)、求证:△ADC≌△CEB.(2)、AD=5cm,DE=3cm,求BE的长度.22. 已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:
(1)、求证:△ADC≌△CEB.(2)、AD=5cm,DE=3cm,求BE的长度.22. 已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题: (1)、在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;(2)、在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,利用(1)的结论,试求∠P的度数;(3)、如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系?并说明理由.23. 一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地的距离为y1(km),快车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为S(km),y1 , y2与x的函数关系图象如图(1)所示,S与x的函数关系图象如图(2)所示:
(1)、在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;(2)、在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,利用(1)的结论,试求∠P的度数;(3)、如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系?并说明理由.23. 一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地的距离为y1(km),快车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为S(km),y1 , y2与x的函数关系图象如图(1)所示,S与x的函数关系图象如图(2)所示: (1)、图中的a= , b= .(2)、求S关于x的函数关系式.(3)、甲、乙两地间依次有E、F两个加油站,相距200km,若慢车进入E站加油时,快车恰好进入F站加油.求E加油站到甲地的距离.
(1)、图中的a= , b= .(2)、求S关于x的函数关系式.(3)、甲、乙两地间依次有E、F两个加油站,相距200km,若慢车进入E站加油时,快车恰好进入F站加油.求E加油站到甲地的距离.